Método de Arquimedes
O primeiro método para calcular p, com alguma precisão, surgiu com Arquimedes. Este começou por perceber que o perímetro de polígonos regulares de n lados inscritos na circunferência é menor que o perímetro da própria circunferência, e que o perímetro de polígonos regulares de n lados circunscritos à circunferência é maior que o da circunferência. E, à medida que aumenta o número de lados dos polígonos regulares, inscritos e circunscritos, estes vão-se assemelhando progressivamente com a circunferência, e, consecutivamente, os seus perímetros vão aproximar-se, como podemos observar na figura 1.
Figura 1
Consideremos então um polígono regular de n lados, circunscrito a um circunferência de raio r. Seguidamente, traçam-se os segmentos de recta que unem o centro da circunferência aos vértices do polígono, obtendo-se assim n triângulos congruentes. E, por construção estes triângulos são isósceles, visto dois dos seus lados serem exatamente o raio da circunferência. Posteriormente, traçam-se segmentos tirados pelo centro perpendicularmente a cada lado. Estes segmentos são as alturas dos n triângulos isósceles em que o polígono foi dividido. Estes triângulos são também iguais entre si , e, qualquer um deles toma no polígono o nome de apótema. Obtemos então um polígono regular constituído por 2n triângulos retângulos congruentes, assim como mostra a figura 2.
Figura 2
Como se pode observar, obtivemos 2n triângulos retângulos, portanto o ângulo A vale 360/2n e um cateto é igual à metade do lado do polígono circunscrito e o outro é o raio da circunferência. Assim, o perímetro do polígono circunscrito (Pc), será igual a 2n vezes p.
Através da figura 3, podemos observar que: P/r = tg Â, logo, P = r . tg(360/2n). Portanto, Pc = 2nr . tg(360/2n).
Como sabemos o perímetro da circunferência é dado por 2pr, então : 2pr < 2nr . tg(360/2n),
ou:
Como sabemos o perímetro da circunferência é dado por 2pr, então : 2pr < 2nr . tg(360/2n),
ou:
assim, p , 3,4641 (2)
Consideremos agora um polígono regular de n lados, inscrito na circunferência de raio r. E, procedendo com o polígono inscrito assim como procedemos com o circunscrito, obtemos mais uma vez, um polígono constituído por 2n triângulos retângulos congruentes.
Figura 4
Como se pode observar na figura 4, o perímetro ( Pi ) do polígono regular inscrito de n lados, pode ser expresso por 2n vezes p. Então, veja a Figura 5:
P = e sen (360/2n), portanto, Pi = 2nr sen(360/2n).
Como o perímetro da circunferência é dado por 2pr, logo temos que:
2pr > 2nr sen(360/2n), então:
2pr > 2nr sen(360/2n), então:
E, em particular para n = 6 temos:
Pelas desigualdades (2) e (4) podemos concluir que, para n = 6 ( hexágono regular)
3 < p < 3,4641
Aumentando progressivamente o número de lados do polígono, obtemos valores, cada vez mais exatos de p.
Usando este método, Arquimedes chegou a aproximações de p, para n = 12, n= 24, n = 48 e por fim para n = 96. Com o polígono regular de 96 lados, Arquimedes demonstrou que:
3,1410 < p < 3,1428
Podemos observar na figura 6, o quadro dos valores obtidos por Arquimedes:
N.º de lados
|
Polígono inscrito
|
Polígono circunscrito
|
6
|
3
|
3,4641
|
12
|
3,1058
|
3,2154
|
24
|
3,1326
|
3,1597
|
48
|
3,1393
|
3,1461
|
96
|
3,1410
|
3,1428
|
Figura 6
Deve-se ter sempre presente que Arquimedes não dispunha do nosso sistema de numeração escrita, mas teve de efetuar todos os cálculos com o sistema de numeração grego.
Arquimedes, como se poderia pensar, não obteve apenas uma fina estimativa para p , mas, levou também muito longe a prática da ideia de integral. No entanto, só cerca de 20 séculos mais tarde, e após muito trabalho nesse sentido, diversas ideias e contribuições de muitos matemáticos se chegou à criação admirável do cálculo integral.
Nota: Existe ainda um outro método para o cálculo do p, que consiste em considerar as áreas dos polígonos regulares. Este outro método tem em conta que, quanto maior for o número de lados do polígono, mais próxima estará a sua área da área do círculo.Os sólidos de Arquimedes, têm o nome de Arquimedes, que os descobriu e relatou em livros que se perderam.
Durante a Renascença, artistas e matemáticos descobriram de novo todos os sólidos de Arquimedes. As descobertas ficaram completas à volta de 1619, por Johannes Kepler, que definiu prismas, antiprismas e poliedros não convexos conhecidos como poliedros de Kepler-Poinsot.
Pesquisado em: www.educ.fc.ul.pt/icm/icm98/icm11/metododearquimedes.htm, em 22?08?2014 as 14h00.






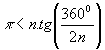





Prezados professores(as), amigos(as), com meu respeito a todos(as) aqui presente, qual o impacto que causaria em afirmar que este enigmático número de π é Racional e Irreversível, uma Matemática Inovadora e impactante no Universo da Matemática, o autor da obra " A ousadia do π ser racional" Sr Sidney Silva.
ResponderExcluir