No estudo da geometria plana e da trigonometria, um dos protagonistas é o triângulo retângulo, pois dele obtemos algumas teorias como Teorema de Pitágoras, relações trigonométricas etc. Mas para que possamos compreender todas essas teorias, primeiramente faz-se necessário entender a composição do triângulo retângulo.
Inicialmente, ele recebe essa classificação de retângulo, pois um de seus ângulos é reto (90°), como podemos constatar na imagem a seguir.
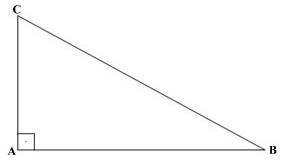
Para entendermos a característica dos outros dois ângulos deste triângulo, façamos a seguinte reflexão: Como a soma dos ângulos internos de um triângulo deve ser 180°, um destes ângulos conhecido é o ângulo reto, logo a soma dos outros dois ângulos deverá ser 90°.
Do raciocínio anterior, conclui-se que os outros dois ângulos devem ser ângulos agudos.
Agora veremos os elementos não menos importantes neste triângulo, que constitui a relação de proporção entre cada ângulo e o lado oposto a este ângulo. No caso do triângulo retângulo, nomeamos os lados de duas maneiras: catetos e hipotenusa.
Dentre os catetos, teremos uma divisão entre: cateto oposto e cateto adjacente, e veremos que para cada ângulo que tomarmos como referência, cada cateto receberá uma classificação em especial.
Neste caso, a hipotenusa sempre será o lado oposto ao ângulo reto, no caso da Figura 1, a hipotenusa é o segmento de reta AB.
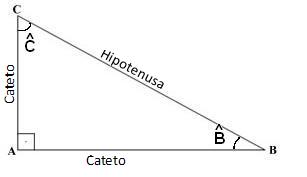
Vamos classificar os catetos deste ângulo: Temos dois catetos (os segmentos AC e BC) que receberão classificação de cateto oposto e cateto adjacente, dependendo do ângulo que tomamos como referência.

Logo: Cateto Oposto: é o lado oposto ao ângulo que se observa, e o Cateto Adjacente: é o lado vizinho ao ângulo que se observa.
O triângulo é o polígono com menor número de lados, mas é uma das formas geométricas mais importantes no estudo da geometria. Sempre intrigou matemáticos desde a Antiguidade. Triângulo retângulo é aquele que apresenta um ângulo interno medindo 90o. Esse tipo de triângulo apresenta propriedades e características muito relevantes. Faremos o estudo das relações entre as medidas dos lados do triângulo retângulo.
Todo triângulo retângulo é composto por dois catetos e uma hipotenusa. A hipotenusa é o maior lado do triângulo retângulo e está oposto ao ângulo reto.
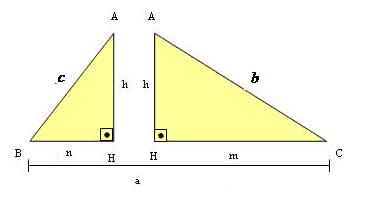
Observe a figura abaixo.
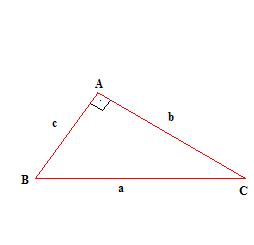
Temos que:
a → é a hipotenusa
b e c → são os catetos.
A perpendicular a BC, traçada por A, é a altura h, relativa à hipotenusa do triângulo.
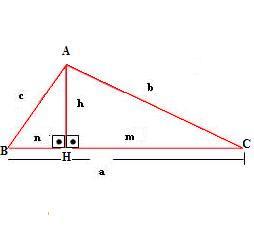
BH = n e CH = m são as projeções dos catetos sobre a hipotenusa.
Os três triângulos são semelhantes
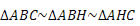
Da semelhança de triângulos obtemos as seguintes relações:
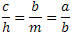
Daí segue que: b2 = am e ah = bc
Temos, também, as seguintes relações:
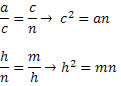
E a mais famosa das relações métricas no triângulo retângulo:
a2 = b2 + c2 Que é o teorema de Pitágoras.
Observe que temos cinco relações métricas no triângulo retângulo:
1. b2 = am
2. ah = bc
3. c2 = an
4. h2 = mn
5. a2 = b2 + c2
Todas elas são de grande utilidade na resolução de problemas que envolvem triângulos retângulos.
Exemplo:-. Determine as medidas da altura relativa à hipotenusa e dos dois catetos do triângulo abaixo.
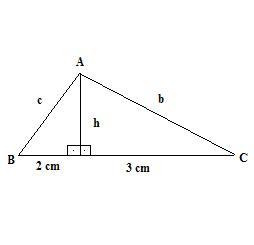
Solução: Temos que: n = 2 cm e m = 3 cm
Utilizando a quarta relação descrita anteriormente, obtemos:
h2 = mn h2 = 3∙2 h2 = 6 h = √6
Segue que: a = 2 + 3 = 5 cm
Daí, utilizando a primeira relação, obtemos:
b2 = am b2 = 5∙3 b2 = 15 b = √15
Da terceira relação, obtemos:
c2 = an c2 = 5∙2 c2 = 10 c = √10
Contido em: http://www.alunosonline.com.br/matematica/relacoes-metricas-no-triangulo-retangulo.html, pesquisado em 05/09/2014 as 10h00.

Nenhum comentário:
Postar um comentário