
Cossecante
Por definição, cossecante é a relação do inverso do seno.
Assim: cossecX = 1/senX
Dado um número real x , tal que x 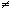 kπ, considerando a reta s tangente
kπ, considerando a reta s tangente ao circulo trigonométrico no ponto P que intercepta o eixo do seno no ponto C, definimos por cossecante o módulo do segmento que vai do centro da circunferência trigonométrica até o ponto C.
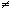 kπ, considerando a reta s tangente
kπ, considerando a reta s tangente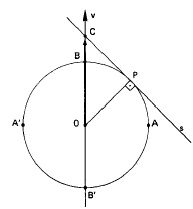
Secante
Por definição temos que secante é a relação do inverso do cosseno.
Assim: secX = 1/cosX
Dado um número real x , tal que x 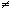 ã/2 + kã , considerando a reta s tangente ao circulo trigonométrico no ponto P que intercepta o eixo do cosseno no ponto C, definimos por secante o módulo do segmento que vai do centro da circunferência trigonométrica até o ponto S.
ã/2 + kã , considerando a reta s tangente ao circulo trigonométrico no ponto P que intercepta o eixo do cosseno no ponto C, definimos por secante o módulo do segmento que vai do centro da circunferência trigonométrica até o ponto S.
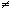 ã/2 + kã , considerando a reta s tangente ao circulo trigonométrico no ponto P que intercepta o eixo do cosseno no ponto C, definimos por secante o módulo do segmento que vai do centro da circunferência trigonométrica até o ponto S.
ã/2 + kã , considerando a reta s tangente ao circulo trigonométrico no ponto P que intercepta o eixo do cosseno no ponto C, definimos por secante o módulo do segmento que vai do centro da circunferência trigonométrica até o ponto S.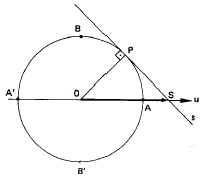
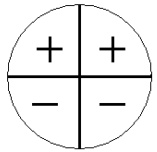
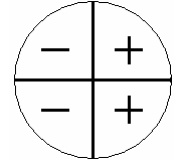
Quando o ângulo é do primeiro ou do quarto quadrante seu sinal é positivo, quando do segundo ou do terceiro seu sinal é negativo.
Cotangente
Por definição temos que cotangente é a relação do inverso da tangente.
Assim: cotgX = 1/tanX = cosX / senX
Dado um número real x , tal que x 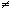 kã, considerando a reta d tangente ao circulo trigonométrico no ponto B seja D o ponto de intersecção da reta d com o segmento OP, definimos por cotangente o módulo do segmento que vai do ponto B até o ponto D.
kã, considerando a reta d tangente ao circulo trigonométrico no ponto B seja D o ponto de intersecção da reta d com o segmento OP, definimos por cotangente o módulo do segmento que vai do ponto B até o ponto D.
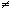 kã, considerando a reta d tangente ao circulo trigonométrico no ponto B seja D o ponto de intersecção da reta d com o segmento OP, definimos por cotangente o módulo do segmento que vai do ponto B até o ponto D.
kã, considerando a reta d tangente ao circulo trigonométrico no ponto B seja D o ponto de intersecção da reta d com o segmento OP, definimos por cotangente o módulo do segmento que vai do ponto B até o ponto D.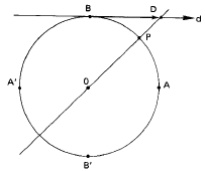
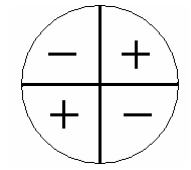
Sinal da cotangente
Quando o ângulo é do primeiro ou do terceiro quadrante seu sinal é positivo, quando do segundo ou do quarto seu sinal é negativo.

As noções básicas da trigonometria sem mistério. Acho que é assim que deve ser uma aula prá início de conversa: simples e direta.Valeu Odair!
ResponderExcluirobrigada, maravilhosa essa explicação.
ResponderExcluirGostei,pois, ajudou-me, bastante!
ResponderExcluirComo vocês chegaram a conclusão da primeira imagem, que representa todas as funções em um único gráfico
ResponderExcluir