Matriz e determinantes são conteúdos estudados dentro de matemática, mas abordados em vários outros ramos, como na informática, engenharia. O estudo dos determinantes depende do conhecimento prévio sobre matrizes.
De uma forma geral podemos dizer que matriz é um conjunto de elementos organizados em linhas e colunas. O número de linhas é representado por m e o número de colunas é representado por n, essas quantidades devem ser maiores ou iguais a um.
A quantidade de linhas de colunas e os elementos que pertencem à matriz são identificados através de uma fórmula.
Determinante é uma matriz quadrada representada de uma forma diferente, pois calculamos o seu valor numérico, o que não acontece com a matriz. Nela aplicamos as quatro operações, ou seja, somamos, multiplicamos, dividimos, subtraímos obtendo outra matriz.
Adição Para adicionarmos duas ou mais matrizes é preciso que todas elas tenham o mesmo número de linhas e de colunas. A soma dessas matrizes irá resultar em outra matriz que também terá o mesmo número de linhas e de colunas.
Os termos deverão ser somados com os seus termos correspondentes.
Concluímos que:
Dada duas matrizes, A e B, as duas de ordem m x n. Então, A + B = C, com
C de ordem m x n ↔ a11 + b11 = c11.
Veja o exemplo abaixo:
Dado a matriz A =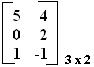 e matriz B =
e matriz B = 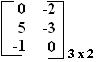 , se efetuarmos a soma dessas matrizes teremos:
, se efetuarmos a soma dessas matrizes teremos:
Somaremos os termos correspondentes em cada matriz:
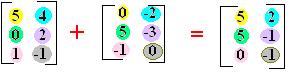
Com a soma das duas matrizes obtivemos outra matriz C =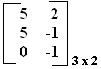 .
.
Subtração
Para efetuarmos a subtração de duas matrizes, as matrizes subtraídas devem ter a mesma ordem (mesmo número de linhas e colunas) e a matriz obtida com a subtração (matriz diferença) também deve ter o mesmo número de linhas e colunas que as matrizes subtraídas.
Cada elemento de uma matriz deve ser subtraído com o elemento correspondente da outra matriz.
Concluímos que:
Dada duas matrizes, A e B, as duas de ordem m x n. Então A – B = C de
ordem m x n ↔ a11 – b11 = c11
Veja o exemplo abaixo:
Dada a matriz A =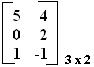 e a matriz B =
e a matriz B = 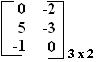 , se efetuamos a subtração dessas matrizes, temos:
, se efetuamos a subtração dessas matrizes, temos:
Subtraindo os termos correspondentes das matrizes:
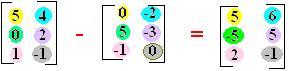
Com a subtração das duas matrizes obtivemos uma matriz C =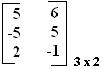
Os termos deverão ser somados com os seus termos correspondentes.
Concluímos que:
Dada duas matrizes, A e B, as duas de ordem m x n. Então, A + B = C, com
C de ordem m x n ↔ a11 + b11 = c11.
Veja o exemplo abaixo:
Dado a matriz A =
Somaremos os termos correspondentes em cada matriz:
Com a soma das duas matrizes obtivemos outra matriz C =
Subtração
Para efetuarmos a subtração de duas matrizes, as matrizes subtraídas devem ter a mesma ordem (mesmo número de linhas e colunas) e a matriz obtida com a subtração (matriz diferença) também deve ter o mesmo número de linhas e colunas que as matrizes subtraídas.
Cada elemento de uma matriz deve ser subtraído com o elemento correspondente da outra matriz.
Concluímos que:
Dada duas matrizes, A e B, as duas de ordem m x n. Então A – B = C de
ordem m x n ↔ a11 – b11 = c11
Veja o exemplo abaixo:
Dada a matriz A =
Subtraindo os termos correspondentes das matrizes:
Com a subtração das duas matrizes obtivemos uma matriz C =
Multiplicação de Matrizes
A multiplicação de matrizes é um processo de cálculos simples, mas que exige alguns cuidados para ser executada com exatidão.
Quando trabalhamos com matrizes, podemos caracterizá-las em relação ao número de linhas e colunas, sendo que identificamos a linha por m e a coluna por n, representando-as, assim, da seguinte forma:
Amxn
Lemos que a matriz A possui m linhas e n colunas. Se, por exemplo, temos uma matriz B com três linhas e quatro colunas, ela será representada como B3x4.
Semelhantemente, cada elemento da coluna é caracterizado pela linha e coluna em que se encontra. A letra i representa sua linha e a j representa sua coluna, portanto, dizemos que o elemento aij está na linha i e na coluna j. Como exemplo, podemos citar o elemento a35, que está localizado na linha 3 e na coluna 5. Vejamos uma representação dos elementos dispostos em uma matriz:
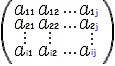
Quando multiplicamos uma matriz por outra, é necessário que o número de colunas da primeira matriz seja igual ao número de linhas da segunda matriz. O resultado dessa multiplicação será uma matriz com o número de linhas da primeira e o número de colunas da segunda. Vejamos:
A m x n . B n x p = C m x p
A multiplicação das matrizes A2 x 3 e B4 x 3 é impossível, pois a primeira possui três colunas e a segunda possui quatro linhas. Como esses valores não são iguais, a multiplicação não ocorre. Agora se pretendemos multiplicar as matrizes A2 x 3 e B3 x 4, além da multiplicação ser totalmente possível, podemos ainda garantir que o produto dessas matrizes será uma matriz A2 x 4.
Ao multiplicarmos uma matriz A por outra matriz B, temos que multiplicar todos os elementos da primeira linha da matriz A pelos elementos da primeira coluna da matriz B e somá-los. Veja como:
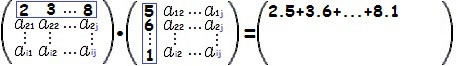
Sendo que a soma (2.5 + 3.6 + … + 8.1) corresponde ao elemento da primeira linha e da primeira coluna da matriz resultante. Repetimos esse processo com todas as linhas e todos as colunas, como podemos ver a seguir no algoritmo da multiplicação de matrizes:
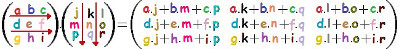
Vamos verificar como ocorre a multiplicação da matriz A e B, sendo:
 e
e 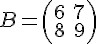
Temos, então:
Vamos agora verificar se a multiplicação é comutativa. Para isso, trocaremos a ordem das matrizes, multiplicando B e A:

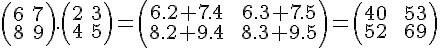
Você observou que A . B é diferente de B . A? Quando trabalhamos com matrizes, a multiplicação não é comutativa.
Vale ressaltar que existe o elemento neutro na multiplicação de matrizes, é a matriz identidade. Esta sempre é quadrada e possui uma diagonal principal formada apenas por “1”, enquanto os demais elementos da matriz são preenchidos por zeros. Qualquer matriz que for multiplicada por uma matriz identidade nunca sofrerá alteração. Vejamos um exemplo:
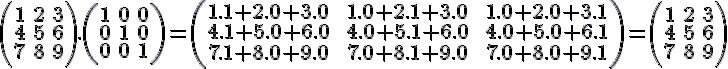
Multiplicação de um número real por uma matriz
Com as matrizes podemos desenvolver várias operações, como: adição e subtração entre matrizes, Potência de matrizes, multiplicação entre matrizes e multiplicação de matriz com número real.
A multiplicação de uma matriz por um número real funciona da seguinte forma: considerando uma matriz qualquer C de ordem mxn e um número real qualquer p.
Quando multiplicamos o número real p pela matriz C encontraremos como produto outra matriz p.C de ordem mxn e seus elementos é o produto de p por cada elemento de C.
Veja o exemplo: Dada a matriz C =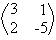 e o número real p = 3. O produto p . C será:
e o número real p = 3. O produto p . C será:
p . C =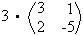
p . C =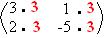
p . C =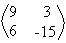
Veja o exemplo que trabalha tanto com a multiplicação de número real por matriz como adição e subtração de matrizes.
Exemplo: Dada as matrizes A =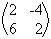 , B =
, B =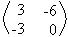 , C =
, C = 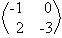 calcule:
calcule:
3A + 2B – 5C
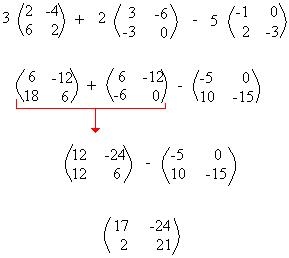
Portanto, 3A + 2B – 5C =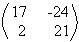 .
.
A multiplicação de uma matriz por um número real funciona da seguinte forma: considerando uma matriz qualquer C de ordem mxn e um número real qualquer p.
Quando multiplicamos o número real p pela matriz C encontraremos como produto outra matriz p.C de ordem mxn e seus elementos é o produto de p por cada elemento de C.
Veja o exemplo: Dada a matriz C =
p . C =
p . C =
p . C =
Veja o exemplo que trabalha tanto com a multiplicação de número real por matriz como adição e subtração de matrizes.
Exemplo: Dada as matrizes A =
3A + 2B – 5C
Portanto, 3A + 2B – 5C =
Contido em: http://www.mundoeducacao.com/matematica/matriz-determinantes.htm, pesquisado em 27/10/2014 as 11h00.

Nenhum comentário:
Postar um comentário