
Vista de Plutão feita pelo telescópio espacial Hubble: defensores clamam que "o tamanho não importa"
Muitas pessoas não entendem por que Plutão deixou de ser um planeta. Plutão foi descoberto em 1930, mas deixou de ser um planeta em 2006, quando foi rebaixado a planeta-anão. Mas qual foi o motivo por trás dessa decisão?
Em 2005 descobrimos um objeto maior do que Plutão, Éris, dividindo um espaço com outros já conhecidos e Plutão, numa região além de Netuno. Esses astros têm características das órbitas ao redor do Sol muito parecidas, sendo bem mais elípticas (alongadas) do que os demais planetas e bastante inclinadas em relação aos demais. Assim, em 2006, os Astrônomos, em mais uma reunião da União Astronômica Internacional (IAU, em inglês), na cidade de Praga, na República Checa, decidiram definir melhor o que é um planeta. Até então era um objeto que girava ao redor de uma estrela, podia ter satélites e tinha massa suficiente para ser esférico.


Até aí Plutão, que foi descoberto em 1930, por um norte-americano – Clyde Tombaugh –, também era considerado um planeta. Mas as novas descobertas sugeriam que deveriam existir vários objetos semelhantes a Plutão além de Netuno. Para que não houvesse uma enxurrada de novos planetas eles preferiram, em uma votação, criar uma nova categoria de objetos do Sistema Solar: os planetas-anões. Além das características mencionadas acima, um planeta deve ter limpado a sua órbita, não dividindo-a com outros objetos além de seus satélites. Plutão, Éris, Makemake e Haumea, além do ex-asteroide Ceres, não estão sozinhos, dividindo a região com outros astros. Assim, eles são classificados como planetas-anões. O nome é um pouco infeliz porque dá a ideia de que é um planeta. Mas é uma nova categoria de objeto. O Sistema Solar é composto atualmente de oito planetas, dezenas de satélites, milhares de asteroides, cinco planetas-anões e milhões de cometas.
Mas, os defensores do "patinho feio" do Sistema Solar não se renderam e inclusive fizeram manifestações pedindo aos cientistas que voltassem a admitir a Plutão no clube dos grandes, clamando que "o tamanho não importa".
Por isso, oito anos depois e a menos de um ano para que aconteça, em Honolulu (Havaí, EUA), a Assembleia Geral da União Astronômica Internacional (IAU), o Centro Harvard-Smithsonian voltou a abrir o debate. Para isso, convidou três especialistas com opiniões diferentes.
O historiador cientista Owen Gingerich, que presidiu o comitê de definição de planetas da IAU, defendeu o status de Plutão como planeta de um ponto de vista histórico e argumentou que "um planeta é uma palavra culturalmente definida que muda com o tempo".
Como pôde a União Astronômica Internacional dizer que Plutão era um planeta anão e depois negar-lhe a posição de planeta? Que era, então, só um anão? Gingerich considera que a IAU fez um "abuso da linguagem" ao tentar definir a palavra planeta e que, por isso, não devia ter expulsado Plutão.
O ponto de vista contrário foi defendido pelo diretor associado do Centro de Planetas Menores, Gareth Williams, que apoiou a exclusão de Plutão e definiu os planetas como "corpos esféricos que orbitam ao redor do sol e que limparam seu caminho", ou seja, que tiraram sua órbita de outros astros.
Por sua vez, o diretor da Iniciativa Origens da Vida de Harvard, Dimitar Sasselov, argumentou que um planeta é "a massa menor esférica da matéria que se forma ao redor das estrelas ou restos estelares", o que, segundo sua opinião, devolve Plutão ao clube planetário.
No final das conferências, um público de todas as idades lembrou seus velhos livros e votou a favor do retorno do antigo nono planeta do Sistema Solar a essa condição.
Na realidade, desde seu descobrimento, em 1930, pelo americano Clyde Tombaugh, Plutão foi objeto de disputas, sobretudo devido a seu tamanho, muito menor que o da Terra, e inclusive que o da Lua.

.jpg)
.jpg)
.jpg)

 e
e 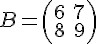

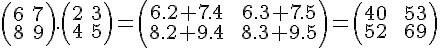
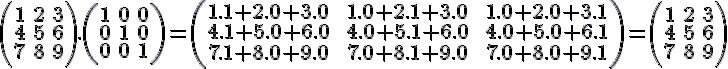
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
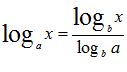




 .
. , sendo que 3 é o logaritmo, 2 é a base e 8 é o logaritmando.
, sendo que 3 é o logaritmo, 2 é a base e 8 é o logaritmando. , sendo que –3 é o logaritmo, 3 é a base e 1/27 é o logaritmando.
, sendo que –3 é o logaritmo, 3 é a base e 1/27 é o logaritmando.







