O número PI

Um número fascinante O número Pi

PI, o valor da razão entre a circunferência de qualquer círculo e seu diâmetro, é a mais antiga constante matemática que se conhece. É também um dos poucos objetos matemáticos que, ao ser mencionado, produz reconhecimento e ate mesmo interesse em praticamente qualquer pessoa alfabetizada.

                                                                    

Apesar da antiguidade do nosso conhecimento do PI, ele ainda é fonte de pesquisas em diversas áreas. Com efeito, dentre os objetos matemáticos estudados pelos antigos gregos, há mais de 2 000 anos, Pi é um dos poucos que ainda continua sendo pesquisado: suas propriedades continuam a ser investigadas e procura-se inventar novos e mais poderosos métodos para calcular seu valor, sendo que a divulgação desses resultados constitui uma das raras ocasiões em que vemos a Matemática atingindo os meios de comunicação de massa. 

Como uma consequência dessa situação, e como uma outra maneira de demonstrar o interesse e fascinação despertados pelo PI, os editores estão sempre a publicar livros dedicados inteiramente ao tema e dirigidos tanto ao grande público como a professores e pesquisadores. Entre os mais recentes, podemos destacar:

• Lennart Berggren (ed) - Pi: A Source Book
  Springer Verlag, 2nd ed., NYork, 2000
  ( nada menos do que 736 paginas! )
• J. P. Delahaye - Le fascinant nombre Pi
  Editions Belin / Pour La Science, Paris, 1997.
• J. Arndt - PI, unleashed.
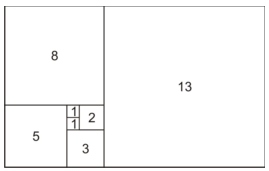
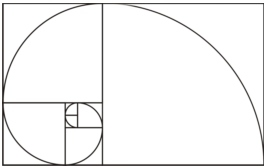
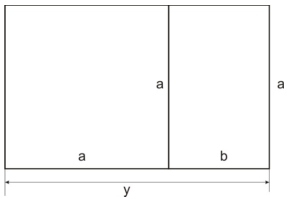
  Springer Verlag, NYork, 2000. PI está em todos os lugares
  
  
  O rolar das ondas numa praia, o trajeto aparente diário das estrelas no céu terrestre, o espalhamento de uma colônia de cogumelos, o movimento das engrenagens e rolamentos, a propagação dos campos eletromagnéticos e um sem número de fenômenos e objetos, do mundo natural e da Matemática, estão associados às idéias de simetria circular e esférica. Ora, o estudo e uso de círculos e esferas, de um modo quase que inexorável, acaba produzindo o PI. Daí a ubiquidade desse número. Ele é uma das constantes universais da Matemática.
  É importante chamarmos a atenção para o fato que também são frequentes as ocorrências do PI em estudos onde aparentemente, principalmente para uma pessoa de pouca formação matemática, não estariam envolvidas simetrias circulares: na normalização da distribuição normal de probabilidades, na distribuição assintótica dos números primos, na construção de números primos próximos a inteiros dados ( na chamada constante de Ramanujan ), e mil e uma outras situações.
  Em verdade, na Geometria Euclidiana, temos quatro constantes que poderiam ser chamadas de PI:

• o PI de circunferências: a constante de proporcionalidade na relação entre a circunferência de um círculo e seu diâmetro
• o PI de áreas de círculos: a constante de proporcionalidade na relação entre a área de um círculo e o quadrado de seu diâmetro
• o PI de áreas de esferas: a constante de proporcionalidade na relação entre a área de uma esfera e o quadrado de seu diâmetro
• o PI de volumes de esferas: a constante de proporcionalidade na relação entre o volume de uma esfera e o cubo de seu diâmetro

Usando as fórmulas clássicas da Geometria, fica muito fácil expressarmos qualquer uma dessas constantes de proporcionalidade em termos das demais. Por questão de tradição, prefere-se trabalhar exclusivamente com o PI da circunferência de círculos, o qual é denotado internacionalmente pela letra pi minúsculo, a letra inicial da palavra grega periferia que significa perímetro ou circunferência ( essa notação surgiu no início do sec. 1700 e foi adotada e popularizada pelo importante livro Análise Infinitesimal, escrito por Euler c. 1750 ).

Aplicações em geometria

 A razão entre o perímetro de um círculo e o seu diâmetro produz o número PI. É um número que mobilizou e ainda mobiliza muitos matemáticos. A principal curiosidade, no caso do PI, é a obtenção de um valor sempre igual e constante, adicionando-se também um mistério: o de não podermos conhecer a última casa. Por esse motivo, o PI passou a ser representado pela letra (do alfabeto grego). Foi uma estratégia para simplificar o registro.

Voltando ao procedimento matemático, que produziu essa misteriosa constante, poderemos igualar as razões entre os perímetros dos círculos e os seus respectivos diâmetros. Essa proporcionalidade permite escrever que o perímetro de uma roda gigante, dividido pelo seu diâmetro, é igual ao perímetro de uma moeda dividido pelo diâmetro dessa mesma moeda:

Na Babilônia, o valor do era considerado igual a três e hoje podemos escrevê-lo com muitas casas depois da vírgula, com as reticências informando que ele não terminou - e não terminará:

3, 14159265358979323846...

Nos livros didáticos, esse número é arredondado para 3,1416 ou 3,14, permitindo cálculos aproximados. No entanto, não podemos esquecer que nunca poderemos afirmar que o valor do é igual a 3,14. Por isso, é essencial que, no cálculo do perímetro, a letra grega apareça para evitar erros:

O perímetro de uma moeda com 1,5 cm de diâmetro pode ser calculado multiplicando-se o diâmetro dessa moeda pela constante . Poderemos registrar como P = 1,5. cm. E se quisermos conferir esse perímetro, contornando a borda dessa moeda com uma linha de costura, teremos que calcular esse perímetro considerando um determinado valor para . Nesse caso, podemos multiplicar 1,5 cm por 3,14, fazendo P = 1,5 x 3,14 - que se aproximará bastante do comprimento da linha. E, portanto, do perímetro.

Se o raio de uma roda de bicicleta é igual a 20 cm, então qual é o comprimento do pneu que contorna essa roda? Responderemos pelo perímetro e obteremos um valor teórico de P = 2 x (20 cm) x = 40 cm ou valor experimental de P = 2 x (20 cm) x 3,14 = 125,6 cm.

Fracionando o círculo para calcular a sua área

O número não aparece somente na fórmula do perímetro do círculo. A área do círculo será um conceito que colocará novamente essa constante em uma das fórmulas mais essenciais da matemática.

Essa fórmula é construída fracionando-se o círculo em uma infinidade de triângulos isósceles, sendo que dois lados deverão ter a mesma medida do raio. Além disso, com a preocupação de que esses triângulos sejam iguais, com a medida da base sendo um pequeno segmento do perímetro desse círculo:

Dois desses triângulos poderão formar um pequeno paralelogramo, com uma inclinação bem pequena tendendo a um retângulo. Quanto menor for a medida da base desses triângulos, que fracionaram o círculo, mais chance teremos de aproximá-los do formato de um retângulo com altura igual ao raio do círculo. Deverão ser colocados em pares, um encostado no outro:

A área de um retângulo é calculada multiplicando-se a medida da sua base pela medida da sua altura. Como cada retângulo é formado por dois triângulos, com a base sendo um pedaço do perímetro do círculo, teremos que imaginar a fragmentação desse círculo em uma quantidade par de triângulos, para que possam ser encaixados dois a dois, sem nenhuma sobra.

Esse encaixe, nesse tipo de quebra-cabeça, formará um retângulo maior com base igual a () x (R) e altura R. É o procedimento de encaixar dois a dois que fará a base do retângulo ter a metade do perímetro do círculo:

Essa base, multiplicada pela altura R do retângulo, será () x (R) x (R) e indicará a área desse retângulo, que poderá ser escrito como raio ao quadrado multiplicado pelo número. Resultado que demonstra que um círculo pode ser transformado em um retângulo, para que a sua área seja deduzida e calculada.

Assim, a fórmula da área do círculo poderá ser escrita como:

A roda da bicicleta, de que falamos acima, com raio igual a 20 cm, além de ter um perímetro igual a 125,6 cm, terá uma área igual a (20 cm) x (20 cm) x (), isto é 400 cm². Além disso, poderá ter um valor aproximado se considerarmos um valor numérico para :                                                     400 x 3,14 = 1256 cm².

São inúmeros os problemas que surgem na matemática envolvendo o perímetro e a área de um círculo. No entanto, talvez o mais importante é percebermos que não podemos estudar geometria sem investigar o número . 

Pesquisado em: http://educacao.uol.com.br/matematica/numero-pi.jhtm, e http://www.mat.ufrgs.br/~portosil/aplcom1a.html  em 18/08/2014 as 10h00.

Aula De Matemática - Tom Jobim

Para quem acha que Matemática é só números, leia e escute o poema cantado por Tom Jobim:

Aula De Matemática

Tom Jobim

Pra que dividir sem raciocinar
Na vida é sempre bom multiplicar
E por A mais B
Eu quero demonstrar
Que gosto imensamente de você

Por uma fração infinitesimal,
Você criou um caso de cálculo integral
E para resolver este problema
Eu tenho um teorema banal

Quando dois meios se encontram desaparece a fração
E se achamos a unidade
Está resolvida a questão

Prá finalizar, vamos recordar
Que menos por menos dá mais amor
Se vão as paralelas
Ao infinito se encontrar
Por que demoram tanto os corações a se integrar?
Se infinitamente, incomensuravelmente,
Eu estou perdidamente apaixonado por você.

Pesquisado em: http://letras.mus.br/tom-jobim/86152/

Fibonacci

O matemático Fibonacci viveu de 1170 a 1250 e na verdade chamava-se Leonardo de Pisa. Filho do diplomata italiano Guilielmo, membro da família Bonacci, Leonardo ficou conhecido como Fibonacci, corruptela de filius Bonacci (filho de Bonacci).

Fibonacci nasceu na Itália, mas foi educado no norte da África, onde seu pai trabalhou por algum tempo. Viajando ao lado de seu pai Fibonacci teve contato com os sistemas numéricos que dariam origem ao nosso sistema hindu-arábico enquanto na Europa os números ainda eram representados apenas pelos algarismos romanos. Fibonacci percebeu as vantagens destes sistemas e, quando regressou à Europa, escreveu sobre eles em seu livro mais famoso, o Liber Abaci, de 1202.

A contribuição de Fibonacci para o conhecimento matemático de sua época foi reconhecida por Frederico II, então imperador do Sacro Império Romano Germânico. Financeiramente, o matemático também foi apoiado por um decreto da República de Pisa que em 1240 outorgou a Fibonacci um salário em reconhecimento aos serviços que havia prestado à cidade através do aconselhamento sobre temas de contabilidade e da transmissão de conhecimentos aos seus cidadãos. Esse decreto é o único documento conhecido que se refere à Fibonacci.
A construção matemática mais famosa atribuída ao matemático é a sequência de Fibonacci, sobre a qual falaremos mais adiante.

Flores e a Sequencia de Fibonacci

As margaridas têm 13, 21 ou 34 pétalas. Os crisântemos têm 34 pétalas. Os girassóis têm suas sementes distribuídas em espirais, normalmente 34 espirais no sentido horário e 55 no sentido anti-horário. O que há de especial com esses números, 13, 21, 34 e 55? São todos números de Fibonacci. O matemático italiano Fibonacci, que viveu entre os anos de 1170 e 1250 é famoso por ter descoberto uma importante sequência numérica, cujos termos são obtidos por uma regra simples: o primeiro número de Fibonacci é 1 e o segundo também é 1. Quanto aos outros termos da sequência, cada um é a soma dos dois termos que o antecedem. A sequência fica assim: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, e assim sucessivamente. Da próxima vez que você vir uma flor, conte suas pétalas! 

UM POUCO ALÉM: O NÚMERO DE ÁUREO 

O que acontece se dividirmos os números da sequência de Fibonacci por seus antecessores? Vamos dar uma olhada...

1/1	=	1
2/1	=	2
3/2	=	1,5
5/3	=	1,666666666666666666...
8/5	=	1,6
13/8	=	1,625
21/13	=	1,615384615384615384...
34/21	=	1,619047619047619047...
55/34	=	1,617647058823529411...
89/55	=	1,618181818181818181...
144/89	=	1,617977528089887640...
233/144	=	1,618055555555555555...
377/233	=	1,618025751072961373...
610/377	=	1,618037135278514588...
987/610	=	1,618032786885245901...
1597/987	=	1,618034447821681864...
2584/1597	=	1,618033813400125234...
4181/2584	=	1,618034055727554179...
6765/4181	=	1,618033963166706529...

Repare que nas últimas divisões os 6 primeiros dígitos já não mudam: 1,61803. Se você continuar dividindo o resultado vai se aproximar cada vez mais de um número irracional chamado de razão áurea (ou número de ouro) e denotado pela letra grega phi.

Este número também tem presença marcada na constituição de diversas plantas. Você pode aprender mais sobre ele em: http://www.uff.br/cdme/rza/ ou http://www.cdme.im-uff.mat.br/rza/

NATUREZA E A SEQUÊNCIA DE FIBONACCI

Há muita polêmica sobre a profusão de aparições da sequência de Fibonacci e do número áureo na natureza, na arquitetura, nas artes, etc. Essa polêmica não é infundada. Em grande parte dos casos difundidos (especialmente com relação às artes e à arquitetura), a suposta presença de números de Fibonacci ou do número áureo não resiste a uma análise mais profunda e cuidadosa. Por isso é muito importante pesar sempre a origem das informações divulgadas e a confiabilidade das fontes de onde foram retiradas.
No caso das plantas, vários estudos de filotaxia confirmam a presença desses números na constituição de certas espécies, como as que citamos na chamada de áudio.

A sequência de Fibonacci é uma sequência numérica construída através de um procedimento recursivo simples:

Os dois primeiros termos são iguais a 1.

Cada novo termo é obtido como a soma dos dois termos precedentes.

Seguindo essas regras, a sequência começa com 1, 1 e para achar o terceiro termo devemos somar estes dois uns:

1, 1, 2.

Para achar o quarto termo, vamos somar os dois termos que o antecedem, isto é, 1 + 2:

1, 1, 2, 3.

Repetindo este procedimento encontramos, pouco a pouco, os termos da sequência:

1, 1, 2, 3, 5.
1, 1, 2, 3, 5, 8.
1, 1, 2, 3, 5, 8, 13

Assim por diante. Aqui estão os primeiros 20 termos da sequência de Fibonacci:

 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765.

Pesquisado em: http://www.uff.br/sintoniamatematica/matematicaenatureza/matematicaenatureza-html/audio-flores-br.html, em 16/08/2014 as 11h00.

Sequência de FIBONACCI

A sequência de Fibonacci é uma sequência numérica construída através de um procedimento recursivo simples:

• Os dois primeiros termos são iguais a 1.
• Cada novo termo é obtido como a soma dos dois termos precedentes.

Seguindo essas regras, a sequência começa com 1, 1 e para achar o terceiro termo devemos somar estes dois uns:

1, 1, 2.

Para achar o quarto termo, vamos somar os dois termos que o antecedem, isto é, 1 + 2:

1, 1, 2, 3.

Repetindo este procedimento encontramos, pouco a pouco, os termos da sequência:

1, 1, 2, 3, 5.
1, 1, 2, 3, 5, 8.
1, 1, 2, 3, 5, 8, 13

Assim por diante. Aqui estão os primeiros 20 termos da sequência de Fibonacci:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765.

O PROBLEMA DOS COELHOS

Fibonacci propôs sua famosa sequência através de um problema curioso que enunciamos a seguir:

Certo homem pôs um casal de coelhos em um lugar totalmente cercado. Quantos casais de coelhos podem ser gerados por esse casal em um ano se supusermos que a cada mês cada casal gera um novo casal, o qual começa a se reproduzir a partir do segundo mês de vida?

Para resolver esse problema podemos montar a seguinte tabela:

Mês	CASAIS MADUROS	CASAIS NOVOS
1	1	0

Veja que no primeiro mês temos apenas um casal maduro. No segundo mês temos, além deste casal, um novo casal, descendente do primeiro par:

Mês	CASAIS MADUROS	CASAIS NOVOS
1	1	0
2	1	1

No terceiro mês esses dois casais já estão na fase reprodutiva e há ainda um novo casal, nascido do primeiro par:

Mês	CASAIS MADUROS	CASAIS NOVOS
1	1	0
2	1	1
3	2	1

Observe que para seguir preenchendo a tabela devemos, para cada mês, fazer o seguinte:

Calculamos o número de casais maduros somando os casais que já eram maduros antes com aqueles que eram casais novos no mês anterior; O número de novos casais a cada mês é exatamente igual ao número de casais maduros no mês anterior.

A tabela completa para um ano fica assim:

Mês	CASAIS MADUROS	CASAIS NOVOS
1	1	0
2	1	1
3	2	1
4	3	2
5	5	3
6	8	5
7	13	8
8	21	13
9	34	21
10	55	34
11	89	55
12	144	89

Logo, em um ano haverá 233 casais de coelhos, sendo que 144 já estarão maduros e 89 serão casais novos. A resposta para a pergunta de Fibonacci é que o primeiro casal dará origem a outros 232 casais. 
Se você observar as colunas do meio e da direita da tabela que montamos, encontrará nelas a sequência de Fibonacci.

Pesquisado em: http://www.uff.br/sintoniamatematica/matematicaenatureza/matematicaenatureza-html/audio-flores-br.html, em 16/08/2014 as 11h00.

Sequência numérica de Fibonacci

O vídeo abaixo mostra um pouco do assunto descrito:

O matemático Leonardo Pisa, conhecido como Fibonacci, propôs no século XIII, a sequência numérica abaixo:

                                  (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...)

Essa sequência tem uma lei de formação simples: cada elemento, a partir do terceiro, é obtido somando-se os dois anteriores, como explicado a seguir: 1+1=2, 2+1=3, 3+2=5 e assim por diante.

Desde o século XIII, muitos matemáticos, além do próprio Fibonacci, dedicaram-se ao estudo da seqüência que foi proposta, e foram encontradas inúmeras aplicações para ela no desenvolvimento de modelos explicativos de fenômenos naturais.

Veja algumas exemplos das aplicação da seqüência de Fibonacci e entenda por que ela é conhecida como uma das maravilhas da Matemática.

A partir de dois quadrados de lado 1, podemos obter um retângulo de lados 2 e 1. se adicionarmos a esse retângulo um quadrado de lado 2, obtemos um novo retângulo 3x2. Se adicionarmos agora um quadrado de lado 3, obtemos um retângulo 5x3. Observe a figura a seguir e veja que os lados dos quadrados que adicionamos para determinar os retângulos formam a sequência de Fibonacci.

Se utilizarmos um compasso e traçarmos o quarto de circunferência inscrito em cada quadrado, encontraremos uma espiral formada pela concordância de arcos cujos raios são os elemento da seqüência de Fibonacci.

O Parthenon que foi construído em Atenas pelo celebre arquiteto grego Fídias. A fachada principal do edifício, hoje em ruínas, era um retângulo que continha um quadrado de lado igual à altura. Essa forma sempre foi considerada satisfatória do ponto de vista estético por suas proporções sendo chamada retângulo áureo ou retângulo de ouro.

Como os dois retângulos indicados na figura são semelhantes temos:

Como:

Substituindo (2) em (1) temos:

Resolvendo a equação:

Logo:

Esse número é conhecido como número de ouro e pode ser representado por:

Todo retângulo em que a razão entre o maior e o menor lado for igual a Φ é chamado retângulo áureo como o caso da fachada do Parthenon.

http://pt.wikipedia.org/wiki/Partenon#mediaviewer/Ficheiro:Parthenon_from_west.jpg

Pesquisado em: http://www.infoescola.com/matematica/sequencia-de-fibonacci/ em 08/08/2014 as 10h00.

O Número de Ouro

  

O que é o número de Ouro ?

O Número de Ouro é um número irracional misterioso e enigmático que nos surge numa infinidade de elementos da natureza na forma de uma razão, sendo considerada por muitos como uma oferta de Deus ao mundo.

 A designação adotada para este número, f (Phi maiúsculo), é a inicial do nome de Fídias que foi escultor e arquitecto encarregado da construção do Pártenon, em Atenas.

Um exemplo desta maravilha é o facto de que se desenharmos um rectângulo cujos lados tenham uma razão ente si igual ao número de Ouro este pode ser dividido num quadrado e noutro rectângulo em que este tem, também ele, a razão entre os dois lados igual ao número de Ouro. Este processo pode ser repetido indefinidamente mantendo-se a razão constante .

A História do número de Ouro

A história deste enigmático número perde-se na antiguidade. No Egipto as pirâmides de Gizé foram construídas tendo em conta a razão áurea : A razão entre a altura de um face e metade do lado da base da grande pirâmide é igual ao número de ouro. O Papiro de Rhind (Egípcio) refere-se a uma «razão sagrada» que se crê ser o número de ouro. Esta razão ou secção áurea surge em muitas estátuas da antiguidade .

Construído muitas centenas de anos depois( entre 447 e 433 a. C.) , o Partenon Grego , templo representativo do século de Péricles contém a razão de Ouro no rectângulo que contêm a fachada (Largura / Altura), o que revela a preocupação de realizar uma obra bela e harmoniosa. O escultor e arquitecto encarregado da construção deste templo foi Fídias. A designação adoptada para o número de ouro é a inicial do nome deste arquitecto - a letra grega f (Phi maiúsculo).

Os Pitagóricos usaram também a secção de ouro na construção da estrela pentagonal.

Não conseguiram exprimir como quociente entre dois números inteiros, a razão existente entre o lado do pentágono regular estrelado (pentáculo) e o lado do pentágono regular inscritos numa circunferência. Quando chegaram a esta conclusão ficaram muito espantados, pois tudo isto era muito contrário a toda a lógica que conheciam e defendiam que lhe chamaram irracional.

Foi o primeiro número irracional de que se teve consciência que o era. Este número era o número ou secção de ouro apesar deste nome só lhe ser atribuído uns dois mil anos depois.

Posteriormente, ainda os gregos consideraram que o rectângulo cujos lados apresentavam esta relação apresentava uma especial harmonia estética que lhe chamaram rectângulo áureo ou rectângulo de ouro, considerando esta harmonia como uma virtude excepcional.

Endoxus foi um matemático grego que se tornou conhecido devido à sua teoria das proporções e ao método da exaustão, criou uma série de teoremas gerais de geometria e aplicou o método de análise para estudar a secção que se acredita ser a secção de ouro.

Uma contribuição preciosa foi-nos dada por Fibonacci ou Leonardo de Pisa.

Fibonacci

No fim da Idade Média havia duas escolas matemáticas: uma,  a escola da igreja e universidade, voltada para um âmbito mais teórico e exaustivo e outra com uma finalidade mais prática e objectiva, a escola do comércio e dos mercadores à qual pertencia Fibonacci.

A contribuição de Fibonacci para o número de ouro está relacionada com a solução do seu problema dos coelhos publicado no seu livro Liber Abaci, a sequência de números de Fibonacci.

É que as sucessivas razões entre um número e o que o antecede vão-se aproximando do número de ouro. Outro matemático que contribuiu para o estudo e divulgação do número de ouro foi Pacioli. Uma curiosidade deste matemático é que foi o primeiro a ter um retrato autêntico.

Publicou em 1509 uma edição que teve pouco sucesso de Euclides e um trabalho com o título De Divina Proportione. Este trabalho dizia respeito a polígonos regulares e sólidos e a razão de ouro.

Leonardo  Da Vinci

Uma contribuição que não pode ser deixada de referir foi a contribuição de Leonardo Da Vinci (1452-1519) . A excelência dos seus desenhos revela os seus conhecimentos matemáticos bem como a utilização da razão áurea como garante de uma perfeição, beleza e harmonia únicas.

É lembrado como matemático apesar da sua mente irrequieta não se concentrar na aritmética, álgebra ou geometria o tempo suficiente para fazer uma contribuição significativa. Representa bem o homem tipo da renascença que fazia de tudo um pouco sem se fixar em nada. Leonardo era um génio de pensamento original que usou exaustivamente os seus conhecimentos de matemática, nomeadamente o número de ouro, nas suas obras de arte. Um exemplo é a tradicional representação do homem em forma de estrela de cinco pontas de Leonardo, que foi baseada nos pentágonos, estrelado e regular, inscritos na circunferência.

Pesquisado em: http://www.educ.fc.ul.pt/icm/icm99/icm17/ouro.htm, em 08/08/2014 as 10h00.