Você gosta de um bom enigma? Então vai gostar desta lista: são 10 exercícios criados para exercitar o cérebro, entre quebra-cabeça, Sudoku e outros menos conhecidos, como Bongard e Fill-a-Pix. Alguns desses enigmas podem ser resolvidos direito na página, outros precisam ser baixados. Mas todos prometem testar suas habilidades e ocupar seus dias.
Enigma 1. O Sudoku mais difícil do mundo
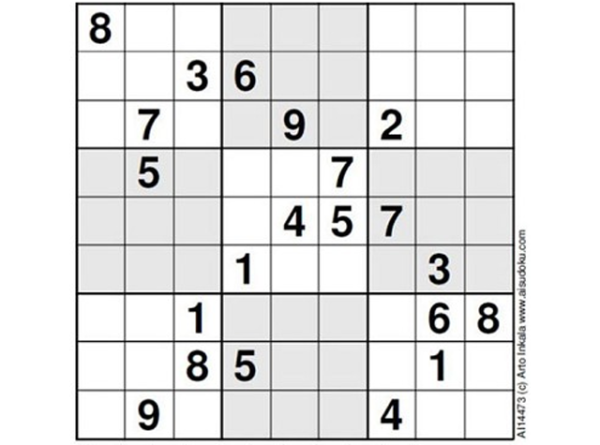
Sudoku é facilmente o quebra-cabeça mais jogado e analisado do mundo; logo, achar um que seja o mais difícil não é tarefa fácil. Mas o matemático finlandês Arto Inkala afirmou ter criado um. De acordo com o jornal britânico The Telegraph, na escala de dificuldade pelo qual os Sudoku são classificados, com uma estrela significando mais simples e cinco estrelas o mais difícil, o enigma acima seria classificado com onze.
Enigma 2. Lógica para quebrar a cabeça
Três deuses – A, B, e C -, em nenhuma ordem particular, são Verdadeiro, Falso e Aleatório. Verdadeiro sempre diz a verdade, Falso sempre fala falsamente, mas se o Aleatório fala verdadeiramente ou falsamente é um assunto completamente aleatório. Sua tarefa é determinar a identidade de A, B, e C fazendo três perguntas de “sim ou não”, e cada questão deve ser dita a exatamente um deus. Os deuses falam inglês, mas vão responder a todas as perguntas em suas próprias línguas, em que as palavras para o sim e não são da e ja, em alguma ordem. Você não sabe qual palavra significa o que.
O lógico e filósofo americano George Boolos inventou o enigma acima, publicado na Revista Harvard de Filosofia, em 1996, e chamou-lhe “o exercício de lógica mais difícil já inventado”.
Enigma 3. Outro modelo de Sudoku
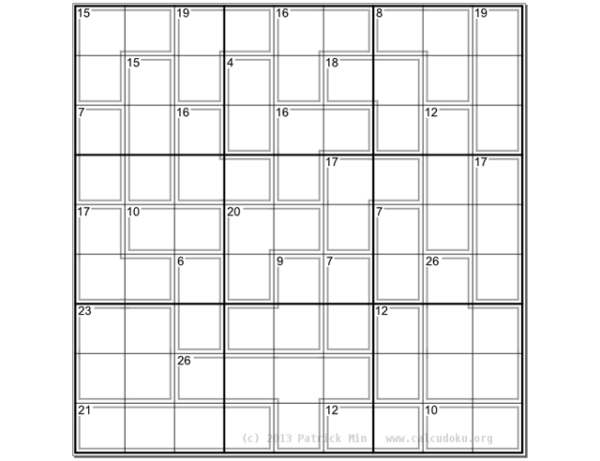
O Killer Sudoku é muito semelhante a um Sudoku, exceto que as pistas são dadas como grupos de células mais a soma dos números dessas células.
Enigma 4. O problema de Bongard
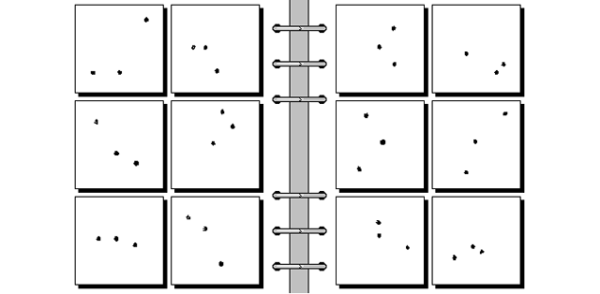
Este tipo de quebra-cabeça apareceu pela primeira vez em um livro do cientista de computação russo Mikhail Moiseevich Bongard em 1967. Para resolver o enigma, você tem que encontrar uma regra em que os 6 padrões do lado esquerdo se adaptem. Os seis padrões a direita não trabalham com esta regra. Por exemplo, o primeiro problema desta página tem como solução: todos os padrões da esquerda são triângulos.
Enigma 5. CalcuDoku
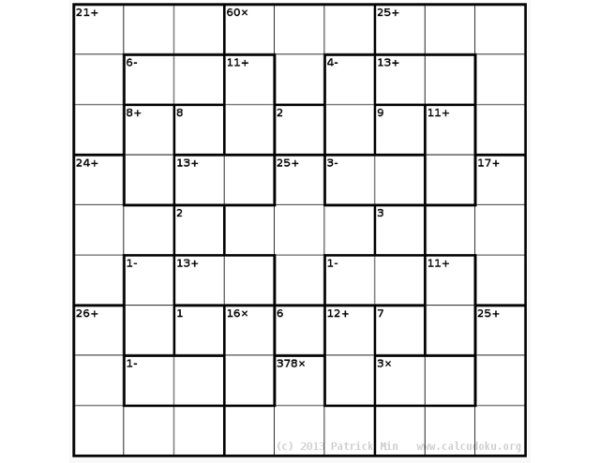
Um CalcuDoku é semelhante a um Killer Sudoku, exceto que (1) qualquer operação pode ser usada para calcular o resultado de uma “gaiola” (não só a adição), (2) o enigma pode ser de qualquer tamanho de quadrado, e (3) a regra do Sudoku que exige os números de 1 a 9 em cada conjunto de células 3 × 3 não se aplica. CalcuDoku foi inventado pelo professor de matemática japonês Tetsuya Miyamoto, que o chamou de “Kashikoku naru” (esperteza).
Enigma 6. Para refletir
O mais difícil exercício “para refletir”: Criar um sistema de armazenamento que codifica 24 bits de informação em oito discos de 4 bits cada, de tal modo que: combinando 8 * 4 bits para um número de 32, a partir de uma função f de 24 bits para 32, pode ser calculado usando apenas cinco operações, cada uma dos quais está fora do conjunto {+, – * , /,%, &, |, ~} (adição, subtração, multiplicação, divisão inteira, modulo, bit a bit e, bit a bit ou e-bit a bit não) em números inteiros de comprimento variável. Em outras palavras, se cada operação leva um nanossegundo, a função pode ser calculada em 5 nanosegundos; e pode-se recuperar os originais de 24 bits, mesmo depois de 2 dos 8 discos falharem.
Enigma 7. Enigma de Kakuro

Kakuro combina elementos de Sudoku, palavras cruzadas, lógica e matemática básica em um único exercício. O objetivo é preencher todos os espaços vazios, utilizando números de 1-9 para a soma de cada bloco horizontal igual a pista à sua esquerda, e a soma de cada bloco vertical igual a pista no seu topo. Além disso, nenhum número pode ser utilizado no mesmo bloco mais do que uma vez.
Enigma 8. Enigma de Martin Gardner
Persistência de um número é o número de passos necessários para reduzi-lo a um único dígito multiplicando todos os seus algarismos para obter um segundo número, depois multiplicando todos os dígitos deste número para se obter um terceiro número, e assim por diante, até que um número de um dígito é obtido. Por exemplo, 77 tem uma persistência de quatro, porque requer quatro etapas para reduzi-lo a um dígito: 77-49-36-18-8. O menor número de persistência 1 é 10, o menor de persistência 2 é 25, o menor de persistência 3 é 39, e o menor de persistência 4 é 77. Qual é o menor número de persistência cinco?
Martin Gardner (1914-2010) foi um popular matemático e escritor americano especializado em ciência matemática recreativa, mas com interesses que abrangiam micromágica, magia de palco, literatura, filosofia, ceticismo científico e religião. Em seu livro “O Livro Colossal de Enigmas Curtos e Problemas”, muitas categorias estão listados em ordem de dificuldade. A descrição acima é do enigma mais difícil do capítulo “Números”.
Enigma 9. Go

Go é um jogo de tabuleiro para dois jogadores que se originou na China mais de 2.500 anos atrás. O jogo é conhecido por ser rico em estratégia, apesar de suas regras relativamente simples. O problema acima é considerado o mais difícil, que tomou 1.000 horas de um grupo de estudantes de alto nível para resolver.
Enigma 10. Fill-a-Pix

Fill-a-Pix é um enigma parecido com Campo Minado, baseado em uma grade com uma imagem pixelada escondida dentro. Usando a lógica por si só, você determina quais espaços são pintados e quais devem permanecer vazios até que a imagem oculta seja completamente exposta. Lógica avançada do Fill-a-Pix, tais como o exercício acima, contém situações onde duas pistas simultaneamente afetam uma a outra, assim como os quadrados em torno dela, tornando estes enigmas extremamente difíceis de resolver.
Fill-a-Pix foi inventado por Trevor Truran, um professor de matemática do ensino médio e ex-editor da Hanjie e várias outras revistas britânicas famosas publicadas pela mídia de enigmas.

Nenhum comentário:
Postar um comentário