Dispositivo Prático de Briot-Ruffini

O dispositivo prático de Briot-Ruffini é uma ótima ferramenta para realizar a divisão de um polinômio qualquer por polinômios do tipo a + x ou a – x.

 
Utilize o dispositivo prático de Briot-Ruffini para realizar divisões entre polinômios

O dispositivo prático de Briot-Ruffini é utilizado para fazer a divisão de polinômios. Para fazer a divisão de um polinômio P(x) por outro polinômio Q(x), utilizando o dispositivo prático de Briot-Ruffini, é fundamental que o polinômio Q(x) seja da forma x + u ou x – u, isto é, deve ser um binômio de 1° grau. Através desse dispositivo, podemos identificar facilmente o quociente e o resto da divisão.

Para utilizar o dispositivo prático de Briot-Ruffini, precisamos primeiramente analisar o polinômio do divisor e encontrar sua raiz. Em seguida, devemos identificar todos os coeficientes numéricos do polinômio do dividendo. Vamos considerar a divisão entre os polinômios P(x) e Q(x), em que P(x) = a₁xⁿ + a₂x^n-1 + a₃x^n-2 +... + a_n-1x¹ + aⁿ e Q(x) = x – u. A raiz do polinômio Q(x) é dada quando ele é igualado a zero. Portanto, a raiz de Q(x) é:

Q(x) = 0
x – u = 0
x = u

Os coeficientes de P(x) são a₁, a₂, a₃, …, a_n-1, a_n. A montagem do dispositivo de Briot-Ruffini a partir da raiz de Q(x) e dos coeficientes de P(x) é dada da seguinte forma:

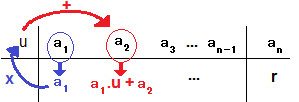
Método de utilização do dispositivo prático de Briot-Ruffini

Para montar o dispositivo de Briot-Ruffini, colocamos a raiz de Q(x) à esquerda e os coeficientes de P(x) à direita, além de reescrever o primeiro coeficiente na linha de baixo. Esse número será multiplicado por u e somado com o segundo coeficiente. O resultado será colocado abaixo do segundo coeficiente como vemos na imagem acima. Em seguida, esse valor encontrado será multiplicado por u e somado com o terceiro coeficiente, e o resultado será colocado abaixo do terceiro coeficiente. Repetimos esse procedimento até que se acabem os coeficientes. O último valor encontrado será o resto da divisão. Os demais valores encontrados na linha inferior serão os coeficientes do polinômio encontrado, lembrando que o último desses valores sempre acompanhará variável cujo expoente é zero.

Vejamos como fazer a divisão de polinômios P(x) por Q(x) quando P(x) = 5x³ – 2x² + 3x – 1 e Q(x) = x – 2. Primeiramente, vamos verificar a raiz de Q(x):

Q(x) = 0
x – 2 = 0
x = 2

Vamos montar o dispositivo de Briot-Ruffini através da raiz de Q(x) e dos coeficientes de P(x):

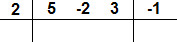
O primeiro coeficiente de P(x) é o 5. Nós podemos reescrevê-lo na linha inferior:

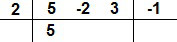
Agora nós multiplicamos o 5 por 2 e somamos o resultado com o segundo coeficiente de P(x), o número – 2, isto é, fazemos 5.2 + (– 2) = 8. O resultado 8 deve ser escrito embaixo do coeficiente – 2.

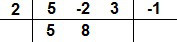
Repetimos o processo, multiplicamos 8 por 2 e somamos com o terceiro coeficiente de P(x), o número 3. O cálculo é dado por 8.2 + 3 = 19. Escrevemos o resultado embaixo do coeficiente 3.

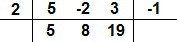
Repetimos o procedimento pela última vez. Agora multiplicamos o 19 por 2 e somamos o resultado com – 1, ou seja, nós fazemos 19.2 + (– 1) = 37. O resultado 37 é colocado embaixo de –1 e é o restode nossa divisão.

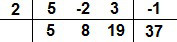
O polinômio resultante dessa divisão é determinado pelos números 5, 8 e 19. Estes são coeficientes desse polinômio. Como fora dito anteriormente, o último número (19) é acompanhado de x⁰, o 8 é acompanhado de x¹, e o 5 é acompanhado de x². Portanto, o polinômio resultante da divisão de 5x³ – 2x² + 3x – 1 por x – 2 é 5x² + 8x + 19, e o resto da divisão é r = 37.

Vejamos outro caso, vamos dividir o polinômio P(x) = 3x⁴ + 5x³ – 11x² + 2x – 3 por Q(x) = x + 3. Aplicando a explicação do método, temos:

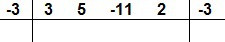
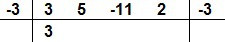
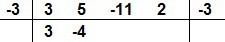
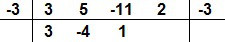
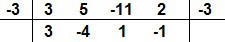
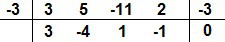
A divisão de P(x) = 3x⁴ + 5x³ – 11x² + 2x – 3 por Q(x) = x + 3 resulta no polinômio 3x³ – 4x² + x – 1, e o resto é 0.

A divisão polinomial pode ser feita ainda através do algoritmo da divisão ou o Teorema de D'Alembert.