HOMOTETIA

A homotetia é um tipo de transformação geométrica que altera o tamanho de uma figura, mas mantém as características principais, como a forma e os ângulos.

Diversos aspectos podem ser analisados para definir se uma figura é semelhante à outra. Por exemplo, em triângulos, há pelo menos quatro casos de congruência. Mas, em geral, é possível afirmar que duas ou mais figuras são semelhantes se elas possuem os mesmos ângulos, a mesma quantidade de lados e alguma proporção entre as medidas dos lados. Uma alternativa apresentada para a construção de figuras semelhantes é a homotetia.

A homotetia é um tipo de transformação geométrica que ficou em segundo plano quando o assunto era semelhança de figuras. Todavia, ela é uma forte aliada para a ampliação ou redução de figuras geométricas. Em geral, quando se aplica a homotetia em algum desenho, as características principais, como a forma e os ângulos, são preservadas; mas o tamanho da figura sofre alterações. Essa relação pode ser explicada através da derivação grega da palavra homotetia, em quehomós significa igual, e thetós, colocado, isto é, as figuras homotéticas são colocadas a uma distância igual a “algo”. Máquinas copiadoras que fazem ampliações ou reduções geralmente utilizam a homotetia como princípio em seu funcionamento. Vejamos a seguir um pouco mais sobre as figuras homotéticas:

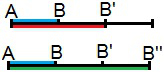
Relação de homotetia entre os segmentos AB, AB' e AB''

Na figura acima, há um segmento AB do qual se deseja criar um segmento partindo de A que tenha o dobro desse segmento. Para isso, cria-se o segmentoAB', destacado em vermelho na figura acima. Dessa forma, pode-se afirmar que:

AB' = 2. AB ou ainda

AB = 1

AB' 2

Nesse caso, há uma homotetia com centro em A. O ponto B' é chamado deimagem (ou homotético) do ponto B.

Caso se desejasse traçar um novo segmento que tivesse o triplo do segmento inicial, haveria o segmento AB'', destacado em verde na figura, que corresponderia ao triplo do comprimento de AB. Sendo assim, entre esses segmentos existiria a seguinte razão:

AB'' = 3. AB ou ainda

AB = 1

AB'' 3

Nesse caso, há uma homotetia com centro em A, e o ponto B'' é a imagem do ponto B ou o homotético do ponto B.

Será que é possível estabelecer uma relação entre AB' e AB''? Se AB' = 2. AB eAB'' = 3. AB, logo:

AB' = 2. AB → AB = 1 . AB'
                       2

AB'' = 3. AB → AB = 1 . AB''
                       3

Portanto:

1 . AB' = 1 . AB''
2            3         

AB' = 2 . AB''
3

A razão entre os segmentos AB' e AB'' é de ⅔.

Veja agora uma relação de homotetia para ampliar um hexágono. Partindo do centro A, há uma homotetia de razão 3, pois o comprimento do segmento AB' é o triplo do segmento AB. É possível perceber que a razão se preserva em relação a todos os outros vértices do hexágono. Apesar do hexágono não ter sofrido alterações em seu formato inicial, a medida de seus lados aumentou três vezes, mas seus ângulos internos permaneceram inalterados.

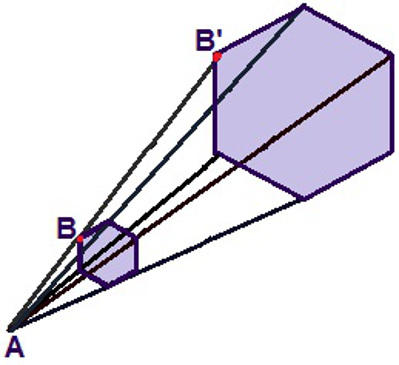
Através de uma relação de homotetia, podemos garantir que os hexágonos são semelhantes, mas o maior tem  três vezes o tamanho do menor

Contido em: http://brasilescola.uol.com.br/matematica/homotetia.htm, pesquisado em 27/05/2016 as 21h00,