
Se as direções forem diversas o choque será oblíquo.

O coeficiente de restituição (e) é uma grandeza adimensional (não tem unidade), por ser calculado pela razão entre duas grandezas de mesma espécie e 0 < e > 1.

 O resultado Vr obtido é sempre em módulo.
O resultado Vr obtido é sempre em módulo. Se houver colisão e os corpos permanecerem unidos após a mesma, ou, se eles se moverem na mesma direção e sentido e com a mesma velocidade, tem-se evidentemente que VX = VY e que Vr= 0.
Se houver colisão e os corpos permanecerem unidos após a mesma, ou, se eles se moverem na mesma direção e sentido e com a mesma velocidade, tem-se evidentemente que VX = VY e que Vr= 0.
Tipos de choques
Nele, a energia é totalmente conservada (é a mesma antes e depois do choque), ou seja, o sistema é conservativo, o coeficiente de restituição é igual a 1 e aquantidade de movimento do sistema á a mesma antes e depois do choque (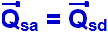 ).
).
Exemplo  se você abandonar de certa altura do solo uma bola e ela retornar à mesma altura, o choque dela com o solo é perfeitamente elástico ou ainda, se a bolase chocar contra uma parede
se você abandonar de certa altura do solo uma bola e ela retornar à mesma altura, o choque dela com o solo é perfeitamente elástico ou ainda, se a bolase chocar contra uma parede
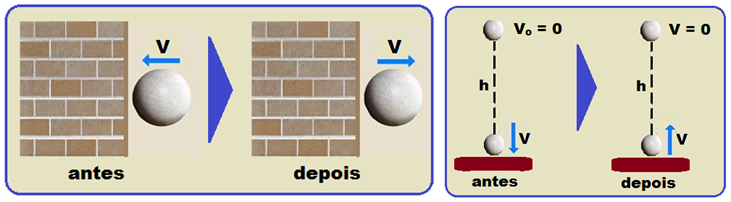
com velocidade de módulo V e retornar na mesma direção e com a mesma velocidade o choque também será perfeitamente elástico.
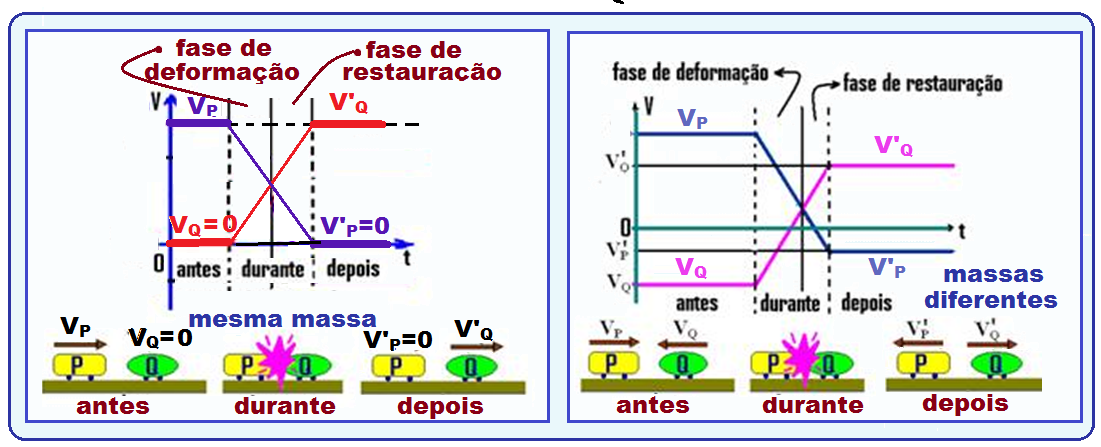
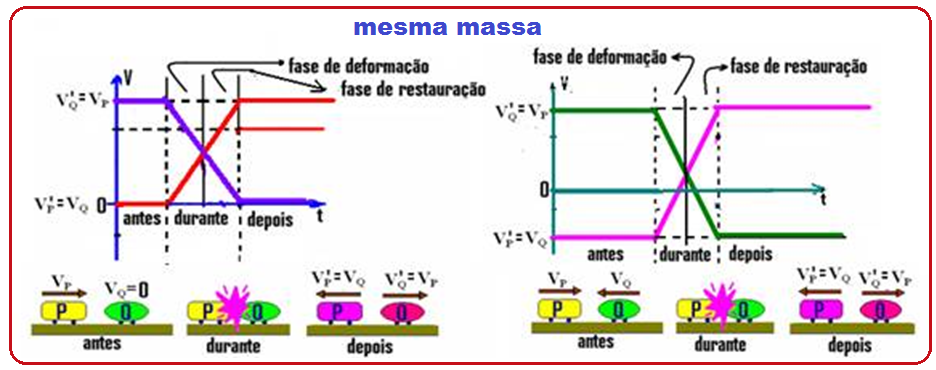
Gráficos de uma colisão perfeitamente elástica
Neste tipo de choque a dissipação de energia é máxima, o coeficiente de restituição é nulo, e,após o choque, os corpos obrigatoriamente se juntam e se movem unidos com a mesma velocidade. Lembre-se de que em qualquer tipo de choque a quantidade de movimento sempre se conserva.
Gráfico da velocidade em função do tempo para a colisão inelástica das figuras abaixo
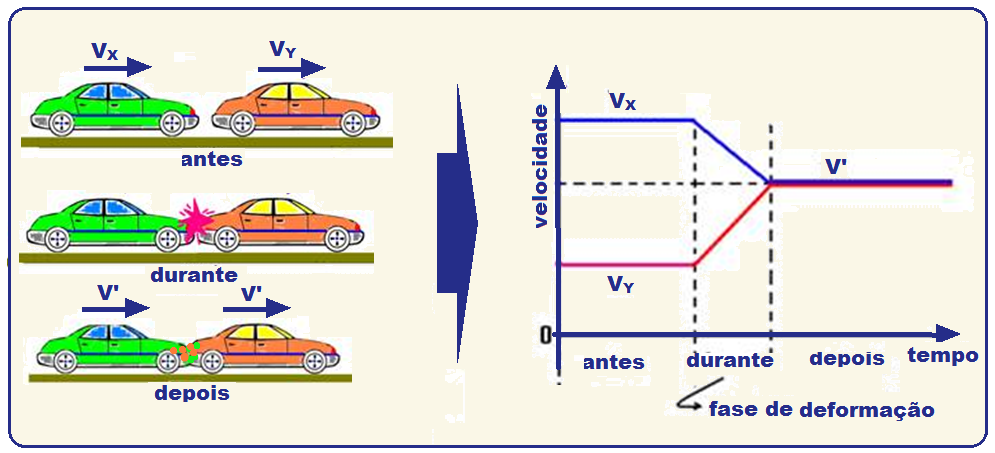
Nesse tipo de choque o sistema é dissipativo com a energia sendo parcialmente dissipada e ocoeficiente de restituição está compreendido entre 0 e 1 (0 < e < 1).Como em qualquer tipo de choque a quantidade de movimento do sistema se conserva.
Gráficos de uma colisão parcialmente elástica
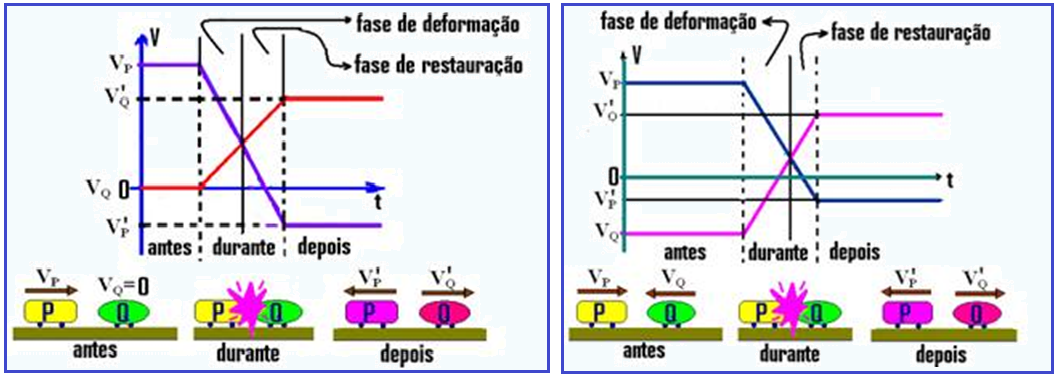
O que você deve saber, informações e dicas

O coeficiente de restituição (e) é uma grandeza adimensional (não tem unidade), por ser calculado pela razão entre duas grandezas de mesma espécie e 0 < e > 1.
 velocidades em sentidos contrários: Vr = VX + VY
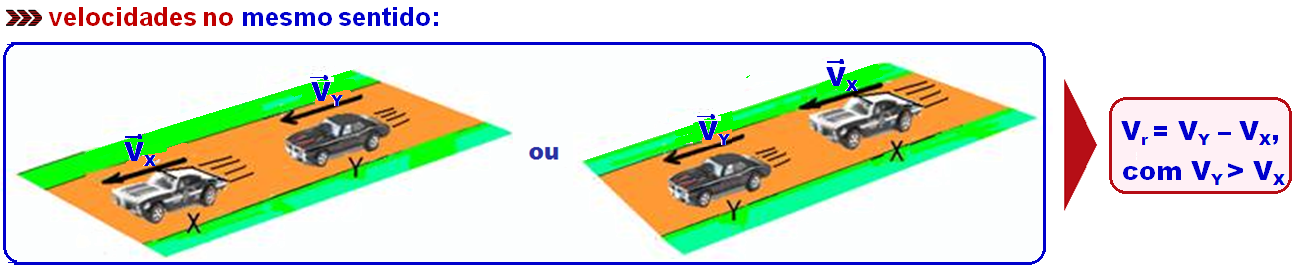
velocidades em sentidos contrários: Vr = VX + VY velocidades no mesmo sentido: Vr = VY – VX, com VY > VX
velocidades no mesmo sentido: Vr = VY – VX, com VY > VX O resultado Vr obtido é sempre em módulo.
O resultado Vr obtido é sempre em módulo.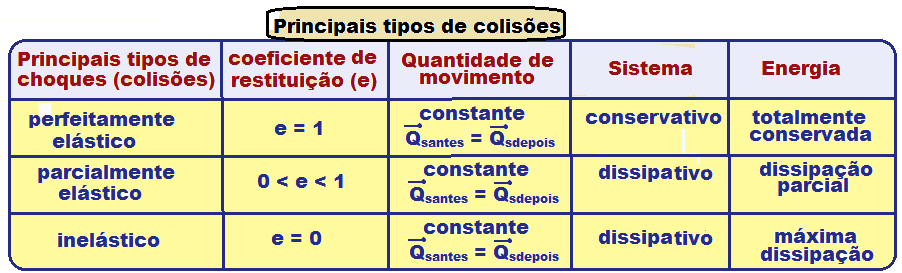
 Em todo choque perfeitamente elástico, se os corpos tiverem a mesma massa, eles trocam suas velocidades.
Em todo choque perfeitamente elástico, se os corpos tiverem a mesma massa, eles trocam suas velocidades.
Exemplos:
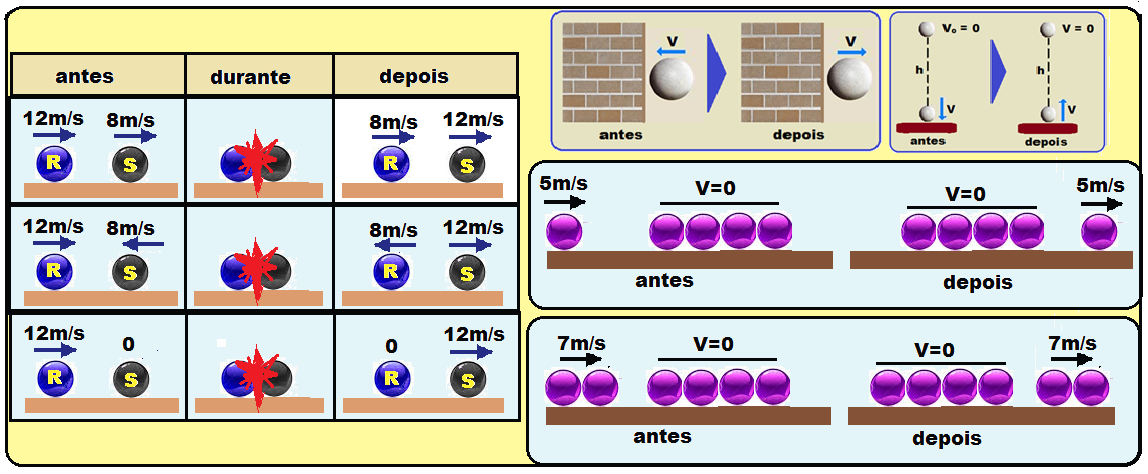
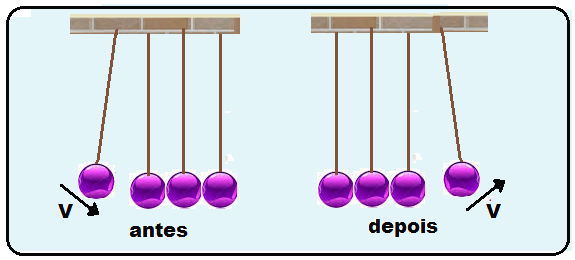
 Exemplos de cálculo do valor do coeficiente de restituição e de classificação de tipos de choques:
Exemplos de cálculo do valor do coeficiente de restituição e de classificação de tipos de choques: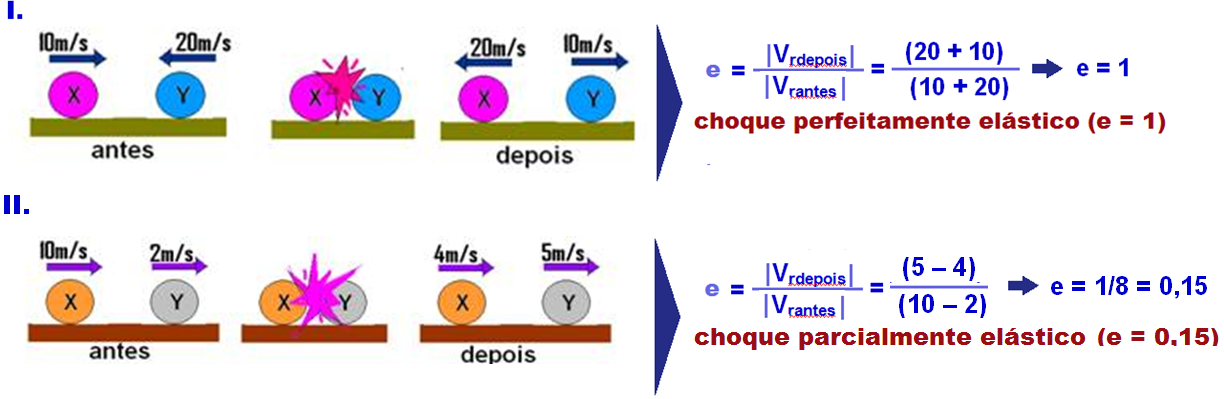

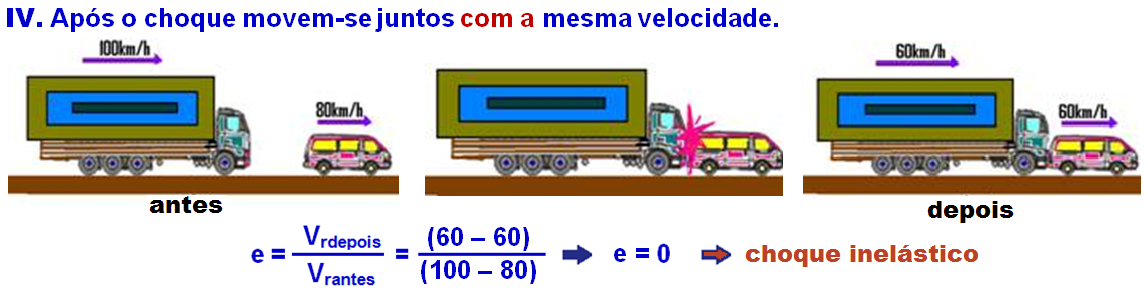

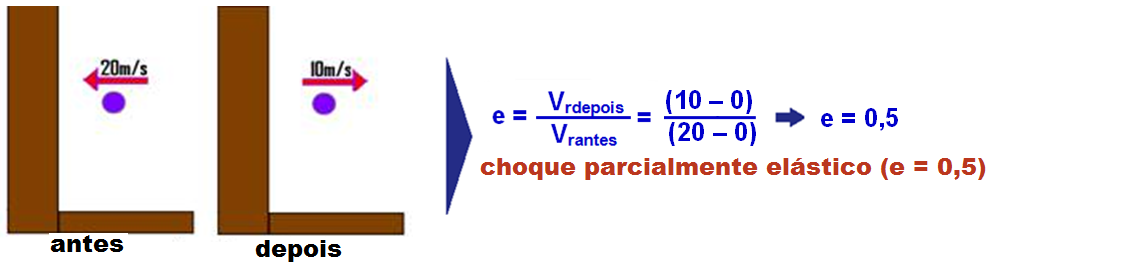
VI. Choque contra um obstáculo fixo (solo)
Esfera abandonada de uma altura H choca-se com o solo e retorna a uma altura h.

VII. Choque de uma pequena esfera (por exemplo, bola de tênis) contra um obstáculo móvel (por exemplo, um ônibus), com:
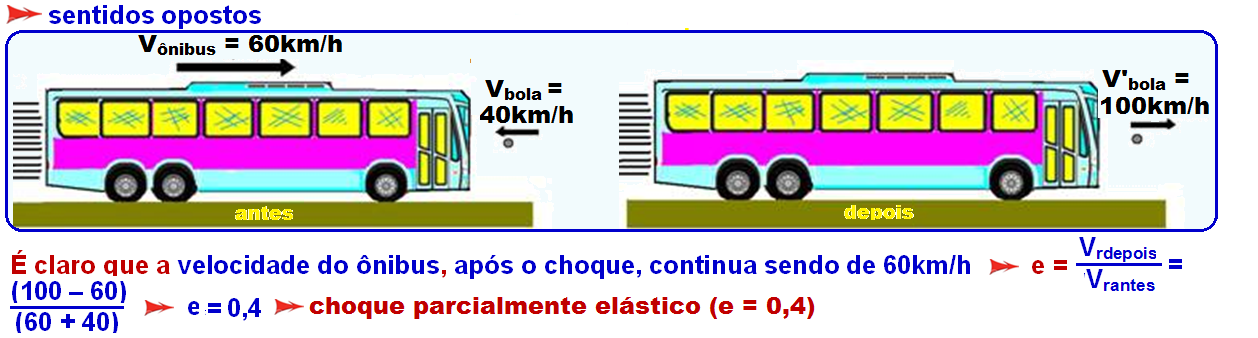
 mesmo sentido
mesmo sentido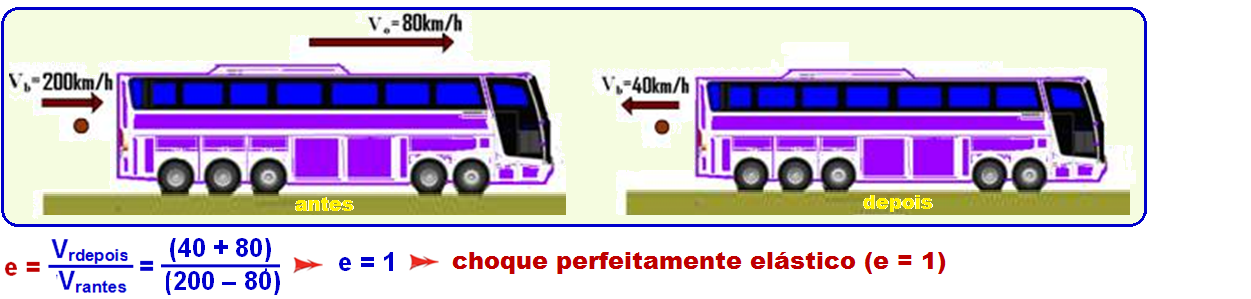
VIII. Como resolver exercícios sobre colisões parcialmente elásticas ou colisões elásticas com massas diferentes:
Etapas
 3a
3a  4a
4a
Exercício exemplo:
Dois móveis P e Q de massas mP = 2kg e mQ = 10kg se movem em sentidos contrários com velocidades VP = 20m/s e VQ = 10m/s e sofrem uma colisãounidimensional parcialmente elásticade coeficiente de restituição igual a 0,8. Calcule suas velocidades após o choque e seus sentidos.
Etapas:
 1a
1a 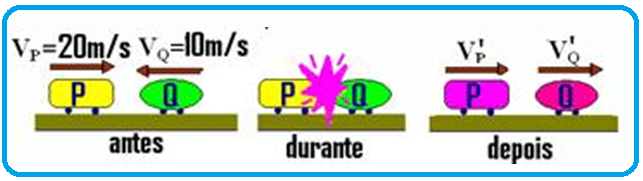
Qa = Qd  mPVP + mQVQ=mPVP’ + mQVQ’
mPVP + mQVQ=mPVP’ + mQVQ’  2.(20) + 10.(-10) = 2.VP’ + 10.VQ’
2.(20) + 10.(-10) = 2.VP’ + 10.VQ’  -60 = 2.VP’ + 10.VQ’
-60 = 2.VP’ + 10.VQ’  Vp’ + 5VQ’= – 30 (equação I)
Vp’ + 5VQ’= – 30 (equação I)
 4a
4a
III  substituindo III em I
substituindo III em I  V’P + 5(24 + V’P) = – 30
V’P + 5(24 + V’P) = – 30  V’P + 120 + 5V’P = – 30
V’P + 120 + 5V’P = – 30  6V’P = – 150
6V’P = – 150 
V’P = – 25m/s (o móvel P, após o choque, se move para a esquerda com velocidade de 25m/s)
VQ’ – VP’ = 24  VQ’ – (-25) = 24
VQ’ – (-25) = 24  V’Q = – 1m/s (após o choque, o móvel Q também se move para a esquerda com velocidade de 1m/s)
V’Q = – 1m/s (após o choque, o móvel Q também se move para a esquerda com velocidade de 1m/s)
Caso particular de colisão perfeitamente elástica (e = 1) com os móveis possuindo mesma massa:
O procedimento é o mesmo que o do exercício anterior:
Exemplo: Dois carrinhos de brinquedo M e N que se movem em sentidos contrários sofrem uma colisão perfeitamente elástica. Suas velocidades antes do choque são VM = 12m/s e VN = 8m/s.Sua massas são iguais (2kg). Determine a intensidade e o sentido de suas velocidades após o choque.
Esquematizando a situação e supondo que após o choque, eles se movam para a direita.

Aplicando o teorema da conservação da quantidade de movimento, supondo velocidades positivas para a direita e negativas para a esquerda  Qa = Qd
Qa = Qd  mN.VN + mM.VM = mN.VN’ + mM.VM’
mN.VN + mM.VM = mN.VN’ + mM.VM’  2.(-8) + 2.(12) = 2.VN’ + 2.VM’
2.(-8) + 2.(12) = 2.VN’ + 2.VM’  -16 +24 = 2.VN’ + 2.VM’
-16 +24 = 2.VN’ + 2.VM’  VN’ + VM’=4 I
VN’ + VM’=4 I
Aplicando a expressão do coeficiente de restituição  e = Vrdepois/Vrantes
e = Vrdepois/Vrantes  1 = (VN’ – VM’)/(12 + 8)
1 = (VN’ – VM’)/(12 + 8)  VN’ – VM’= 20 II
VN’ – VM’= 20 II
Resolvendo o sistema composto por I e II  VN’=12m/s (para a direita) e VM’= – 8m/s (para a esquerda).
VN’=12m/s (para a direita) e VM’= – 8m/s (para a esquerda).
Observe que, após o choque, M transferiu a N sua velocidade de 12m/s para a direita e que N transferiu a M sua velocidade de 8m/s para a esquerda. Assim, pode-se concluir que:
“Em todo choque perfeitamente elástico, se os corpos tiverem a mesma massa eles obrigatoriamente trocam suas velocidades”
Contido em: http://fisicaevestibular.com.br/novo/mecanica/dinamica/colisoes-mecanicas-ou-choques-mecanicos/, pesquisado em 31/10/2015 as 9hoo.

Nenhum comentário:
Postar um comentário