Conjunto é um conceito primitivo desenvolvido pelo matemático George Cantor. A partir dele se desenvolveu diversos outros estudos matemáticos.
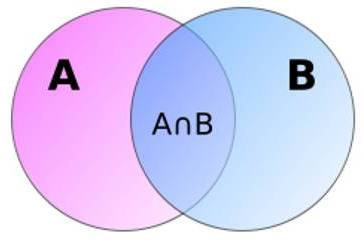
Elementos de um conjunto e suas representações
Na Matemática existem alguns conceitos que não se definem. Eles constituem a base de todas as outras definições que são estudadas em Matemática. A exemplo disso, há a reta, o ponto e o plano. Você consegue definir um ponto? Um ponto não precisa de uma definição, mas a partir dele há todo o estudo da Geometria. Semelhantemente acontece com os “Conjuntos”, um conceito matemático primitivo que não apresenta definição.
Ao questionar qualquer criança a respeito do que é um conjunto, ela pode ter dúvidas para responder a essa pergunta, mas provavelmente não terá em mente um exemplo de conjunto. Por exemplo, um pote de doces pode caracterizar um conjunto de balas ou ainda uma banda pode ser descrita como um conjunto de músicos. Da mesma maneira, pode-se dizer que os números {0, 2, 4, 6, 8, 10…} formam um conjunto de números pares.
No final do século XIX, o matemático George Cantor (1845-1918) deu início ao estudo da Teoria dos Conjuntos. Um conjunto pode ser considerado bem definido quando é possível identificar os seus componentes. No exemplo anterior, poderíamos dizer que o número 20 faz parte do conjunto? Vamos analisar esse elemento: o número 20 é par? Sim, então o número 20 faz parte do conjunto dos números pares. Podemos simplificar a linguagem chamando o conjunto dos números pares de P. Então:
P = {conjunto dos números pares} ⇒ P= {0, 2, 4, 6, 8, 10...}
Podemos ainda afirmar que o número 20 pertence a esse conjunto da seguinte forma:
20 € P
Tente agora imaginar um conjunto formado apenas pelos múltiplos de 5, vamos chamá-lo de Q. Temos, então:
Q = {0, 5, 10, 15...}
Nesse caso, o 20 pertence ao conjunto Q? Ele é múltiplo de 5? Sim, pois 4*5=20, então 20 é múltiplo de 5 e, portanto, pertence a Q. Mas existem outros números que pertencem ao conjunto dos números pares e dos múltiplos de 5 simultaneamente. Podemos melhor representá-los através do Diagrama de Venn, como na imagem abaixo:
.jpg)
Na parte roxa estão representados os números que fazem parte apenas do conjunto P; na seção verde, há os que fazem parte apenas do conjunto Q; e, na parte laranja, estão os números que fazem parte tanto do conjunto P quanto do Q. Dizemos que os números 0, 10 e 20 pertencem à intersecção dos conjuntos P e Q, isto é,{0,10,20} € P ᴨ Q.
A concepção do conjunto numérico pode ser compreendida a partir da compreensão de um conjunto. Os conjuntos numéricos foram concebidos conforme surgiam mudanças na matemática.
Para desenvolver a matemática hoje estudada, inúmeras mudanças na organização de todos os conceitos matemáticos foram necessárias. A concepção dos conjuntos numéricos recebeu maior rigor em sua construção com Georg Cantor, que pesquisou a respeito do número infinito. Cantor iniciou diversos estudos sobre os conjuntos numéricos, constituindo, assim, a teoria dos conjuntos.
A construção de todos os conjuntos numéricos que hoje possuímos parte de números inteiros usados apenas para contar até os números complexos que possuem vasta aplicabilidade nas engenharias, nas produções químicas, entre outras áreas.
Definir conjunto é algo tão primitivo que se torna uma tarefa difícil. Entretanto, compreendemos conjunto como uma coleção de objetos, números, enfim, elementos com características semelhantes.
Sendo assim, os conjuntos numéricos são compreendidos como os conjuntos dos números que possuem características semelhantes. Nesta seção, a concepção desses conjuntos será abordada, visando à compreensão dos elementos que constituem cada um dos conjuntos numéricos.
Temos então os seguintes conjuntos numéricos:
 );
); );
); );
); );
); );
); )
)
Nenhum comentário:
Postar um comentário