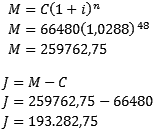Critérios para identificação de arranjo ou combinação
Os exercícios de análise combinatória podem ser resolvidos por arranjo ou combinação, mas como identificar qual dos dois agrupamentos o exercício está se referindo? Para isso é preciso que coloquemos em prática alguns critérios que ajudarão nessa identificação.Esses critérios são aplicados da seguinte forma: Em um problema de análise combinatória iremos encontrar vários agrupamentos, monte pelo menos um deles e modifique a ordem dos elementos desse agrupamento.
Se depois da mudança tiver formado um agrupamento diferente, esse problema será de arranjo.
Se depois da mudança tiver formado o mesmo agrupamento, esse problema será de combinação, ou seja, mesmo se os elementos em ordem diferentes continuar identificando o mesmo agrupamento.
Veja como funciona a aplicação desse critério:
Considere nove pontos diferentes de uma circunferência, conforme a figura.
Quantas retas ficam determinadas por esses nove pontos?
Pra descobrir se o exercício é de arranjo ou combinação é preciso que montemos pelo menos um dos agrupamentos (reta).
Uma reta é formada por, no mínimo, 2 pontos e, como os pontos não são colineares podemos unir qualquer ponto, assim podemos dizer que (A,B) é um agrupamento, se trocarmos a ordem dos seus elementos (B,A) a reta (agrupamento) continua sendo a mesma, portanto, esse exercício será resolvido por combinação.
Assim, aplicamos a fórmula da combinação, sendo que n = 9 e p = 2.
C9,2 = 9!____
2! (9-2)!
C9,2 = 9 . 8 . 7!
2 . 1 . 7!
C9,2 = 72
2
C9,2 = 36
Serão formados com os 9 pontos da circunferências 36 retas.
As principais ferramentas da Análise Combinatória são a Permutação, o Arranjo e a Combinação, mas muitos estudantes se confundem na hora de decidir qual delas utilizar para resolver um problema específico. Aqui, vamos explicar as características de cada uma e quando devem ser utilizadas.
Uma permutação de n elementos distintos é um agrupamento ordenado desses elementos. Pode ser calculada pela fórmula Pn=n!. Ela deve ser utilizada quando você quiser contar quantas possibilidades existem de se organizar um número de objetos de forma distinta, por exemplo:
- O número de anagramas da palavra LIVRO é uma permutação de 5 elementos, calculada através de 5+ = 5 . 4 . 3 . 2 . 1 = 120, pois para a primeira posição você pode colocar 5 letras; para a segunda, restaram 4, para a terceira, 3 e assim por diante;
- O número de filas que podem ser formadas com 25 pessoas é 25!, pois para o primeiro lugar da fila temos 25 possibilidades, para o segundo 24 e assim por diante.
Um arranjo de n elementos dispostos p a p, com p menor ou igual a n, é uma escolha de p entre esses n objetos na qual a ordem importa. Sua fórmula é dada por:
A(n,p) = n! / (n-p)!
O exemplo mais clássico de arranjo é o pódio: em uma competição de 20 jogadores, quantas são as possibilidades de se formar um pódio com os três primeiros lugares? Note que, neste problema, queremos dispor 20 jogadores em 3 lugares, onde a ordem importa, afinal o pódio formado por João, por Marcos e por Pedro não é o mesmo formado por Pedro, por Marcos e por João. Outro exemplo é o número de possibilidades de se formar uma foto com n pessoas. Perceba que as permutações nada mais são do que casos particulares de arranjos onde n = p.
As Combinações de n elementos tomados p a p são escolhas não ordenadas desses elementos, calculadas por:
C(n,p) = n! / p! (n-p)!
Um exemplo clássico é quando queremos formar uma comissão de 3 pessoas escolhidas entre 10 pessoas. Diferentemente do pódio do exemplo anterior, uma comissão formada por João, por Pedro e por Maria é a mesma comissão formada por Maria, por Pedro e por João.
Por fim, fique com essa frase de impacto:
“Uma escolha ordenada significa escolher e colocar em ordem”,
ou, matematicamente: A = C . P
“Uma escolha ordenada significa escolher e colocar em ordem”,
ou, matematicamente: A = C . P
Contido em: http://www.mundoeducacao.com/matematica/criterios-para-identificacao-arranjo-ou-combinacao.htm, e http://www.andremachado.org/artigos/440/entenda-a-diferenca-entre-permutacao-arranjo-e-combinacao.html, pesquisado em 09/11/2014 as 13h00.

 , sendo sempre n e Ώ a quantidade de elementos do evento e do espaço amostral respectivamente.
, sendo sempre n e Ώ a quantidade de elementos do evento e do espaço amostral respectivamente.

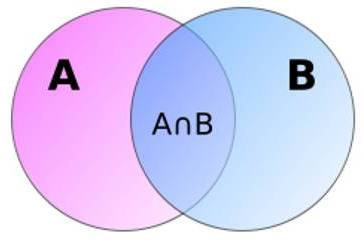
.jpg)

 );
); );
); );
); );
); );
); )
)