Conjuntos Numéricos

Definição de Conjuntos Numéricos

Ao agrupamento de elementos com características semelhantes damos o nome de conjunto. Quando estes elementos são números, tais conjuntos são denominados conjuntos numéricos.

Neste tópico estudaremos os cinco conjuntos numéricos fundamentais, que são os conjuntos numéricos mais amplamente utilizados.

Conjunto dos Números Naturais

Em algum momento da sua vida você passou a se interessar por contagens e quantidades. Talvez a primeira ocorrência desta necessidade, tenha sido quando lá pelos seus dois ou três anos de idade algum coleguinha foi lhe visitar e começou a mexer em seus brinquedos. Provavelmente, neste momento mesmo sem saber, você começou a se utilizar dos números naturais, afinal de contas era necessário garantir que nenhum dos seus brinquedos mudasse de proprietário e mesmo desconhecendo a existência dos números, você já sentia a necessidade de um sistema de numeração.

Em uma situação como esta você precisa do mais básico dos conjuntos numéricos, que é o conjunto dos números naturais. Com a utilização deste conjunto você pode enumerar brinquedos ou simplesmente registrar a sua quantidade, por exemplo.

Este conjunto é representado pela letra N (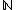 ). Abaixo temos uma representação do conjunto dos números naturais:

As chaves são utilizadas na representação para dar ideia de conjunto. Os pontos de reticência dão a ideia de infinidade, já que os conjuntos numéricos são infinitos.

Este conjunto numérico inicia-se em zero e é infinito, no entanto podemos ter a representação de apenas um subconjunto dele. A seguir temos um subconjunto do conjunto dos números naturais formado pelos quatro primeiro múltiplos de sete:

Para representarmos o conjunto dos números naturais, ou qualquer um dos outros quatro conjuntos fundamentais, utilizamos o caractere asterisco após a letra, como em 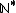. Temos então que:

Conjunto dos Números Inteiros

Mais adiante na sua vida em uma noite muito fria você tomou conhecimento da existência de números negativos, ao lhe falarem que naquele dia a temperatura estava em dois graus abaixo de zero. Curioso você quis saber o que significava isto, então alguém notando o seu interesse, resolveu lhe explicar:

Hoje no final da tarde já estava bastante frio, a temperatura girava em torno dos 3° C, aí ela desceu para 2° C, continuou esfriando e ela abaixou para 1° C e uma hora atrás chegou a 0° C. Se a temperatura continuava a abaixar e já havia atingido o menor dos números naturais, como então representar uma temperatura ainda mais baixa?

Com exceção do zero, cada um dos números naturais possui um simétrico ou oposto. O oposto do 1 é o -1, do 2 o -2 e assim por diante. O Sinal "-" indica que se trata de um número negativo, portanto menor que zero. Os números naturais a partir do 1 são por natureza positivos e o zero é nulo.

O zero e os demais números naturais, juntamente com os seus opostos formam um outro conjunto, o conjunto dos números inteiros e é representando pela letra Z (  ).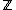

A seguir temos uma representação do conjunto dos números inteiros:

Note que diferentemente dos números naturais, que embora infinitos possuem um número inicial, o zero, os números inteiros assim como os demais conjuntos numéricos fundamentais não têm, por assim dizer, um ponto de início. Neste conjunto o zero é um elemento central, pois para cada número à sua direita, há um respectivo oposto à sua esquerda.

Utilizamos o símbolo 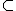 para indicar que um conjunto está contido em outro, ou que é um subconjunto seu, como o conjunto dos números naturais é um subconjunto do conjunto dos números inteiros, temos que .

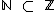Podemos também dizer que o conjunto dos números inteiros contém ( 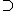 ) o conjunto dos números naturais ( ).

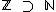Como supracitado podemos escrever 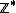 para representarmos o conjunto dos números inteiros, mas sem considerarmos o zero:

Com exceção do conjunto dos números naturais, com os demais conjuntos numéricos fundamentais podemos utilizar os caracteres "+" e "-" como abaixo:

Note também 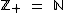que  e que .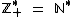

Conjunto dos Números Racionais

Esperto por natureza você percebeu que havia mais alguma coisa além disto. No termômetro você viu que entre um número e outro existiam várias marcações. Qual a razão disto?

Foi-lhe explicado então que a temperatura não muda abruptamente de 20° C para 21° C ou de -3° C para -4° C, ao invés disto, neste termômetro as marcações são de décimos em décimos. Para passar de 20° C para 21° C, por exemplo, primeiro a temperatura sobe para 20,1° C, depois para 20,2° C e continua assim passando por 20,9° C e finalmente chegando em 21° C. Estes são números pertencentes ao conjunto dos números racionais.

Números racionais são todos aqueles que podem ser expressos na forma de fração. O numerador e o denominador desta fração devem pertencer ao conjunto dos números inteiros e obviamente o denominador não poderá ser igual a zero, pois não há divisão por zero.

O número 20,1 por exemplo, pode ser expresso como , assim como 0,375 pode ser expresso como 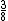 e 0,2 por ser representado por .

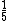Note que se dividirmos quatro por nove, iremos obter 0,44444... que é um número com infinitas casas decimais, todas elas iguais a quatro. Trata-se de uma dízima periódica simples que também pode ser representada como 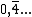, mas que apesar disto também é um número racional, pois pode ser expresso como .

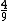O conjunto dos número racionais é representado pela letra Q (  ).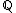

O conjunto dos números inteiros é um subconjunto do conjunto dos números racionais, temos então que .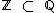

Facilmente podemos intuir que 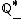 representa o conjunto dos números racionais negativos e que  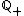representa o conjunto dos números racionais positivos ou nulo.

Abaixo temos um conjunto com quatro elementos que é subconjunto do conjunto dos números racionais:

A realização de qualquer uma das quatro operações aritméticas entre dois números racionais quaisquer terá como resultado também um número racional, obviamente no caso da divisão, o divisor deve ser diferente de zero. Sejam a e bnúmeros racionais, temos:

Conjunto dos Números Irracionais

Então mais curioso ainda você perguntou: "Se os números racionais são todos aqueles que podem ser expressos na forma de fração, então existem aqueles que não podem ser expressos desta forma?"

Exatamente, estes números pertencem ao conjunto dos números irracionais. Provavelmente os mais conhecidos deles sejam o número PI ( 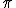 ), o número de Euler (  ) e a raiz quadrada de dois ( 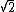 ). Se você se dispuser a calcular tal raiz, passará o restante da sua existência e jamais conseguirá fazê-lo, isto porque tal número possui infinitas casas decimais e diferentemente das dízimas, elas não são periódicas, não podendo ser expressas na forma de uma fração. Esta é uma característica dos números irracionais.

A raiz quadrada dos números naturais é uma ótima fonte de números irracionais, de fato a raiz quadrada de qualquer número natural que não seja um quadrado perfeito é um número irracional. 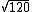 é um número irracional, pois 120 não é um quadrado perfeito, ou seja, não há um número natural que multiplicado por ele mesmo resulte em cento e vinte, já  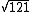é um número natural, pois .

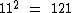A letra I ( 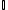 ) representa o conjunto dos número irracionais.

Utilizando o caractere especial "*", por exemplo, podemos representar o conjunto dos números irracionais desconsiderando-se o zero por .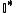

O conjunto abaixo é um subconjunto do conjunto dos números irracionais:

Diferentemente do que acontece com os números racionais, a realização de qualquer uma das quatro operações aritméticas entre dois números irracionais quaisquer não terá obrigatoriamente como resultado também um número irracional. O resultado poderá tanto pertencer a 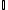, quanto pertencer a .

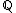Conjunto dos Números Reais

Acima vimos que um número natural também é um número inteiro ( 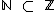 ), assim como um número inteiro também é um número racional (  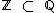), portanto .

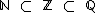Vimos também que os números racionais não estão contidos no conjunto dos números irracionais e vice-versa. A intersecção destes conjuntos resulta no conjunto vazio: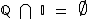 

A intersecção é uma operação por meio da qual obtemos um conjunto de todos os elementos que pertencem simultaneamente a todos os conjuntos envolvidos. Sejam dois conjuntos 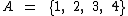 e 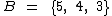, a intersecção entre estes dois conjuntos será .

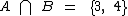O conjunto dos números reais é representado pela letra R ( 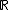 ) e é formado pela união do conjunto dos números racionais com o conjunto dos irracionais, que simbólicamente representamos por: .

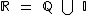A união é uma operação por meio da qual obtemos um conjunto de todos os elementos que pertencem ao menos a um dos conjuntos envolvidos. Sejam dois conjuntos 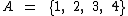 e 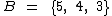, a união entre estes dois conjuntos será .

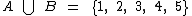O conjunto dos números racionais está contido no conjunto dos números reais ( 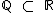 ), assim como o conjunto dos números irracionais também é subconjunto do conjunto dos números reais (  ).

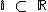Através dos caracteres especiais "+" e "*", por exemplo, podemos representar o conjunto dos números reais positivos por .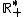

Abaixo temos um exemplo de conjunto contendo número reais:

Conjuntos Numéricos Fundamentais em Diagrama

Abaixo temos a representação dos conjuntos numéricos fundamentais em um diagrama.

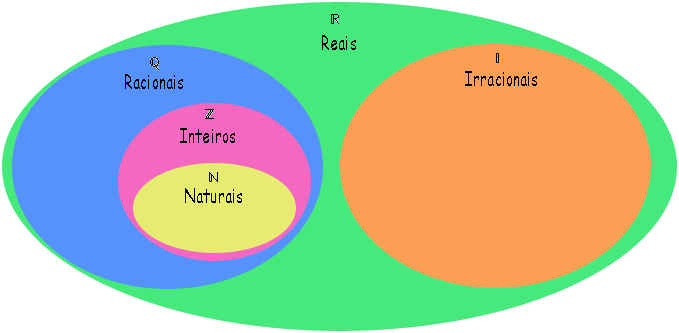
Através deste diagrama podemos facilmente observar que o conjunto dos números reais ( 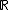 ) é resultado da união do conjunto dos números racionais como o conjunto dos números irracionais (  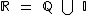). Observamos também que o conjunto dos números inteiros está contido no conjunto dos números racionais (  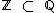) e que os números naturais são um subconjunto do números inteiros (  ).

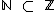Como podemos ver, os diagramas nos ajudam a trabalhar mais facilmente com conjuntos. Ainda neste diagrama rapidamente identificamos que os números naturais são também números reais ( 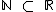 ), mas não são números irracionais (  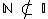), isto porque o conjunto dos números irracionais não contém o conjunto dos números naturais (  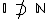), mas sim o conjunto números dos racionais que os contém (  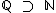), assim como o conjuntos dos números reais (  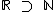) e dos inteiros (  ).

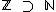Contido em: http://www.matematicadidatica.com.br/ConjuntosNumericosFundamentais.aspx; pesquisado em 08/12/2014 as 15h00.

Radiciação

A radiciação é o processo de se extrair raízes de um número. Representamos por , onde n é denominado índice da raiz e x é chamado radicando e a é definido como a raiz. Dentre as raízes mais conhecidas estão as quadradas e as cúbicas, porém é possível extrair muitas outras raízes de um número. Quando estamos calculando uma raiz quadrada, podemos omitir o índice, assim  correspondem ao mesmo número.

Raiz quadrada

A raiz quadrada de um número positivo, x, corresponde também a um número positivo que, quando elevado ao quadrado, é igual ao número x. Confuso? Não! Basta notar que se =a, então temos que a²=x. Por exemplo:  pois 3²=9. Mas poderíamos pensar também em -3, já que (-3)²=9. Então recorremos à definição acima e lembramos que a raiz quadrada é sempre um número positivo. Assim .

Quando a resposta de uma raiz quadrada é um número racional, dizemos que a raiz é exata. Sempre que a resposta não for exata, temos um número irracional. Por exemplo:  é um número racional. Mas  é irracional e pode ser aproximado por 1,41.

Raiz cúbica

No caso das raízes cúbicas, não precisamos que sejam somente números positivos, podemos ter resultados negativos também, mas a ideia de cálculo é a mesma. Assim, temos que , já que 2³=8 e também , já que (-2)³=-8.

Assim como as raízes quadradas, as raízes cúbicas podem ser exatas ou não exatas. E, da mesma forma, se a resposta for exata temos um número racional e se for não exata temos um número irracional. Por exemplo:  é um número racional e  é irracional.

Raiz n-ésima

Os mesmos cálculos realizados nos casos de raízes quadradas e cúbicas podem ser estendidos pra qualquer índice n. Assim, quando denotamos  queremos obter a raiz n-ésima de x. Apesar de o índice ser maior, a fórmula de cálculo é a mesma para as situações anteriores. Então, se queremos encontrar  basta calcular o número que elevado a n-ésima potência seja igual a x. Se , temos que .

Também é possível obter respostas que sejam números racionais ou números irracionais, vai depender se as raízes forem exatas ou não.

Propriedades

Para qualquer número natural n>1, temos:

Exemplos:

Contido em:http://www.brasilescola.com/matematica/radiciacao.htm; pesquisado em 08/12/2014 as 15h00. 

Potenciação

Definição: Potenciação ou Exponenciação significa multiplicar um número real  (base) por ele mesmo X vezes, onde X é a potência (número natural). Exemplo:

3² (leia-se "três elevado ao quadrado", ou "três elevado à segunda potência" ou ainda "três elevado à dois").

No exemplo, precisamos multiplicar o 3 por ele mesmo. Ficando: 3.3 = 9.

Então 3³ = 3 . 3 . 3 = 3 . 9 = 27

Algumas outras definições que podem ser utilizadas:

a¹ = a
a⁰ = 1, a ≠ 0

Propriedades

1 - Multiplicação de potências de bases iguais = mantenha a base e some os expoentes:

aⁿ . a^m = a^n+m

2 - Divisão de potências de bases iguais - mantenha a base e subtraia os expoentes:

(aⁿ) / (a^m) = a^n-m , "a" diferente de zero.

3 - Potência de potência = mantenha a base e multiplique os expoentes:

(a^m)ⁿ = a^{m . n}

Atenção

As potências abaixo NÃO são iguais:

(a^m)ⁿ

e

a^mn

na primeira, resolvemos o que está entre parênteses primeiro, já na segunda, nós devemos elevar m à n, e depois elevar a  ao resultado da operação anterior.

4 - (a . b)ⁿ = aⁿ . bⁿ

5 - (a/b)ⁿ = aⁿ/bⁿ , "b" diferente de zero.

Potenciação com números negativos

Observe os exemplos abaixo:

(-3)² = 9
-3² = -9

O sinal de negativo ( - ) na frente do três, só fará parte da potenciação quando estiver dentro de um parêntese, caso contrário, ele continua no seu lugar no resultado.

Porém, no primeiro exemplo, o expoente é 2, número par, por isto o negativo do 3 ao final se transforma em positivo. Se fosse 3, o resultado seria negativo:
(-3)³ = (-3) . (-3) . (-3) = 9 . (-3) = -27

se tirarmos os parênteses

-3³ = - 3 . 3 . 3 = -9 . 3 = -27

Contido em: http://www.infoescola.com/matematica/potenciacao-exponenciacao/; pesquisado em 08/12/2014 as 15h00.

Regra de Cramer para resolução de sistemas

Sabemos que sistema linear é um conjunto de n equações lineares com n incógnitas relacionadas entre si. A solução de um sistema linear pode ser obtida de várias maneiras. Veremos uma das formas de resolução de um sistema utilizando a regra de Cramer.
Todo sistema linear pode ser associado a uma matriz envolvendo os coeficientes numéricos e a parte literal. Por exemplo, considere o seguinte sistema linear:

Sua representação matricial dos coeficientes das incógnitas é (matriz incompleta):

Já a representação matricial completa do sistema, levando em consideração somente os coeficientes numéricos, é:

Todo o sistema pode ser representado matricialmente da seguinte forma:

Diante da relação existente entre um sistema linear e uma matriz, Cramer desenvolveu um método de resolução de sistemas envolvendo as propriedades das matrizes e dos determinantes.
A regra de Cramer diz que: os valores das incógnitas de um sistema linear são dados por frações cujo denominador é o determinante da matriz dos coeficientes das incógnitas e o numerador é o determinante da matriz dos coeficientes das incógnitas após a substituição de cada coluna pela coluna que representa os termos independentes do sistema.

Vejamos um exemplo para melhor compreensão da regra de Cramer.

Exemplo: Encontre a solução do sistema abaixo utilizando a regra de Cramer.

Solução: Primeiro, devemos escrever a matriz que representa os coeficientes das incógnitas e obter seu determinante.

Em seguida, devemos excluir a primeira coluna da matriz dos coeficientes das incógnitas e substituí-la pelos termos independentes do sistema 12, 12 e – 16, e calcular o determinante.

Agora, fazemos o mesmo com a segunda coluna da matriz dos coeficientes das incógnitas.

Calculando o determinante dessa matriz, obtemos:

Repetindo o mesmo procedimento para a terceira coluna da matriz dos coeficientes das incógnitas, obtemos:

Fazendo o cálculo do determinante, teremos:

Segundo a regra de Cramer, temos que:

Assim, o conjunto solução do sistema é S = {(3, 4, 5)}

Contido em:  http://www.alunosonline.com.br/matematica/regra-cramer-para-resolucao-sistemas.html, pesquisado em 08/12/2014 as 14h30min.

Determinante de uma matriz - ordem 1, 2 ou 3

Podemos calcular o determinante de qualquer matriz desde que essa seja quadrada, ou seja, que a matriz tenha o mesmo número de linhas e de colunas (seja uma matriz de ordem n x n).

Podemos dizer que determinante de uma matriz quadrada é o seu valor numérico.

Os elementos de uma matriz podem ser colocados entre parênteses, colchetes ou entre duas barras duplas; e os elementos dos determinantes são colocados entre duas barras.

Matriz de ordem 1

Quando uma matriz possui apenas um elemento ou possui apenas uma linha e uma coluna, dizemos que essa matriz é de ordem 1. Veja alguns exemplos:

Se A = [10], então o seu determinante será representado assim: det A = |10| = 10

Se B = (-25), então o seu determinante será representado assim: det B = |-25| = -25

Podemos concluir que o determinante de ordem 1 terá o seu valor numérico sempre igual ao seu elemento..

Matriz de ordem 2

Dada a matriz A de ordem dois A =  , o seu determinante será calculado da seguinte forma:

O determinante de ordem dois possui uma diagonal principal e uma diagonal secundária.



O cálculo do seu valor numérico é feito pela diferença do produto da diagonal principal com o produto da diagonal secundária.

det A = = - 3 – (- 10) = - 3 + 10 = 7

Matriz de ordem 3

Dada a matriz de ordem 3, B = o valor numérico do seu determinante é calculado da seguinte forma:

Primeiro representamos essa matriz em forma de determinante e repetimos as duas primeiras colunas.

det B =

Depois calculamos os produtos das diagonais principais e os produtos das diagonais secundárias.

det B =

Deve-se pegar o oposto dos produtos das diagonais secundárias e somar com os produtos das diagonais principais.

Det B = – (0 + 40 + 0) –15 + 0 – 4 = – 40 – 19 = – 59

Essa regra utilizada no cálculo do determinante de matriz de ordem 3 é chamada de Regra de Sarrus.

Contido em: http://www.mundoeducacao.com/matematica/determinante-matriz-ordem-1-2-ou-3.htm, pesquisado em 08/12/2014 as 14h00.