Físicos observam novo estado da matéria em um material inesperado

TECNOLOGIA

Em abril, a comunidade física foi surpreendida quando cientistas anunciaram terem feito a primeira observação direta de um estado completamente novo de matéria – conhecido como líquido de spin – pela primeira vez.

Agora, uma nova equipe de físicos recentemente sugeriu ter observado o mesmo estado, mas desta vez em um material onde supostamente deveria ser impossível. Tal descoberta poderia mudar a compreensão atual que temos de como fazer computação quântica.

Segundo o pesquisador Christian Balz, do Helmholtz-Zentrum Berlin für Materialien und Energie (HZB), na Alemanha, ele e sua equipe provaram empiricamente que os estados quânticos de líquido de spin “podem ocorrer em cristais consideravelmente mais complexos com diferentes constelações de interações magnéticas”. Logo, de acordo com uma das pesquisadoras, Bella Lago, isso poderia ser importante para o avanço dos computadores quânticos no futuro “porque os líquidos de spin são um dos possíveis blocos de construção para levar a uma menor unidade de informação quântica, conhecido como um qubit”.

 O conceito de spin (giro/rotação) no mundo quântico não significa um elétron que está fisicamente em giro, mas sim a um tipo de momento angular intrínseco que simplesmente descreve como esse elétron está se comportando. Na computação quântica, isso é simplificado ao dizer que um estado de spin baixo, alto ou em superposição (ambos ao mesmo tempo). Logo, o líquido de spin quântico é um estado da matéria que ocorre quando o spin de dois elétrons continua flutuando de maneira líquida, livremente, e em temperaturas muito baixas, mesmo quando deveriam estar congelados. A previsão dessa teoria foi feita em 1973, mas só foi observada pela primeira vez neste ano, em um material bidirecional semelhante ao grafeno.

 O critério utilizado pelos cientistas é que um material deve ter interações antiferromagnéticas – ou antiparalelas –, que é o oposto das interações ferromagnéticas observadas em materiais como o ferro e o níquel. Assim, se há um elétron de spin baixo, o outro próximo a ele deverá ter um spin alto, e assim por diante. Diferente disso, os materiais antiferromagnéticos não necessariamente precisam entrar em estado de spin líquido a menos que eles tenham um arranjo atômico triangular, o que torna esse alinhamento impossível.

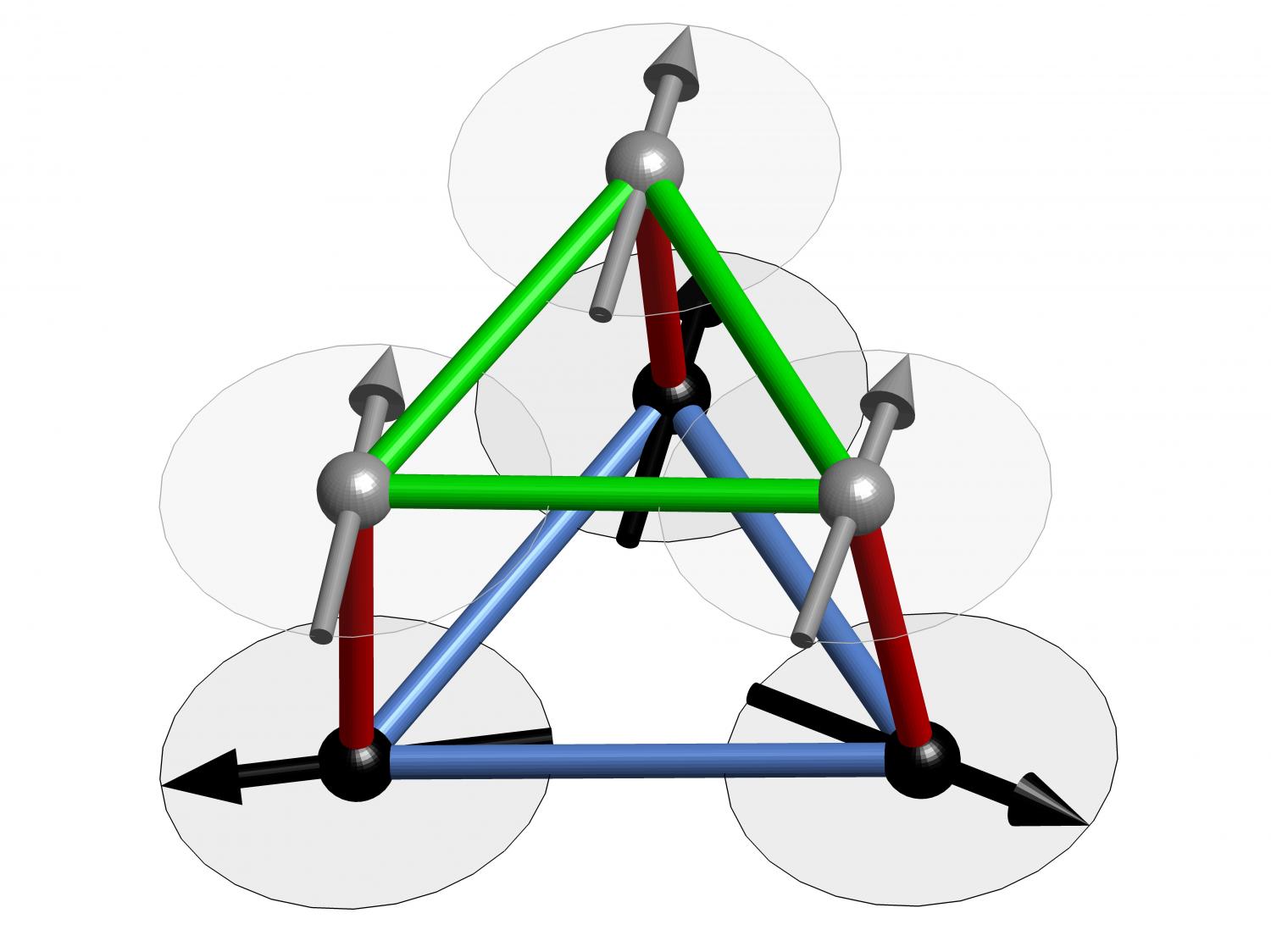
Imagem: Reprodução / HZB

Você pode imaginar agora três átomos dispostos em cada ponta de um triângulo – eles nunca estarão em alinhamentos paralelos porque conforme um muda sua posição, o outro automaticamente mudará também. Logo, eles irão manter esse alinhamento em uma temperatura de zero absoluto e, portanto, um estado líquido de spin.

Contudo, o novo estudo sugere que esses critérios não estão tão corretos, porque conseguiram observar o mesmo estado da matéria em um material que não se encaixa nesse perfil: o monocristal de óxido de cromo cálcico (Ca10Cr7O28). Composto por treliças Kagome – nomeado assim em razão da semelhança com os padrões das treliças japonesas. Basicamente, isso significa que o material tem uma mistura complexa de interações antiferromagnéticas, mas também fortes interações ferromagnéticas que, de acordo com a teoria convencional, deve evitar o comportamento de spin líquido.

A equipe conseguiu provar que o estado mencionado estava de fato ocorrendo e em temperaturas extremamente baixas – cerca de -273 graus Celsius. Para explicar isso, eles sugeriram uma hipótese de que o material poderia se comportar como um líquido de spin sem acabar como nosso entendimento convencional do estado da matéria. Assim, a partir de simulações numéricas, eles mostraram que a razão para isso é a concorrência, ou seja, diferentes interações magnéticas em materiais que estão competindo uns com os outros, e mantendo os spins em movimento ao redor.

 De acordo com Lake, “o trabalho expande nossa compreensão de materiais magnéticos, e também nos mostra que há potencialmente muito mais candidatos para líquidos de spin do que o esperado”.

Agora, a pesquisa, publicada na revista Nature Physics, precisará ser verificada por outros cientistas antes de ser capaz de afirmar com certeza que o estado de líquido de spin pode de fato ocorrer em diferentes tipos de materiais.

Contido em: http://www.jornalciencia.com/liquido-de-spin/,, pesquisado em 28/07/2016 as 10h00.

Os segredos dos melhores professores de matemática do mundo

Método de ensino de Xangai, cidade mais populosa da China,vem se espalhando por escolas europeias.

Kevin Doyle   Da BBC

Os professores de matemática de Xangai, na China, estão entre os melhores do mundo graças ao do alto desempenho de seus alunos em exames internacionais.

A reputação deve-se ao método empregado pelos docentes, que se tornou um dos principais produtos de exportação da cidade mais populosa da China - metade das escolas no Reino Unido, por exemplo, devem adotar o "sistema de ensino de Xangai".

Os estudantes de Xangai, por exemplo, estão três anos à frente dos de outros países em termos de escolaridade.Estatísticas comprovam que alunos do ensino fundamental que aprendem matemática usando a técnica têm rendimento superior aos demais.

Mas qual é o segredo do sucesso da cidade? A BBC compilou os princípios do método - bem como suas críticas.

Conceito é tudo
O método de Xangai estrutura cada aula em torno de um único conceito matemático - como aprender adições básicas, resolver uma equação ou entender as frações como parte de um todo.

E tudo é coberto muito metodicamente, de modo que a aula não avança até que cada estudante tenha entendido.

"Em muitas partes do mundo, acredita-se que uma boa aula é aquela que cobre grande parte da ementa do dia, ou seja, quanto mais se avança, melhor", diz Mark Boylan, especialista em educação da Universidade Sheffield Hallam, do Reino Unido, e colaboradora da publicação Schools Week.

"Em Xangai, o objetivo é assegurar que um conceito seja totalmente aprendido e não seja ensinado de novo no futuro."

Especialistas em matemática consideram o sistema muito rigoroso ou exigente, baseado em manuais feitos sob medida que substituem folhetos ou planilhas.

Trata-se de uma metodologia altamente conceitual, na medida em que professores baseiam suas aulas em métodos fundamentais e leis da matemática, embora os alunos sejam encorajados a representar fisicamente os conceitos usando objetos e imagens para ajudá-los a visualizar ideias abstratas.

Além disso, a forma como os alunos falam e escrevem sobre matemática, acreditam os especialistas, pode contribuir para seu sucesso.

"Sempre lhes pedimos para explicar a resposta em frases completas. Ou seja, não adianta escrever apenas a resposta certa, mas entender o conceito. Essa é a chave para construir o raciocínio lógico e a linguagem matemática", informa o programa de desenvolvimento profissional Mathematics Mastery, baseado no método asiático.

Por outro lado, críticos dizem que o sistema é muito abstrato e não aplica a matemática em cenários da vida real.

Alguns também argumentam que o método ensina os alunos a se preparar para provas, ou seja, a ter um bom desempenho nos exames internacionais, mas sem adaptar o conhecimento a situações do dia a dia.

Unidos venceremos
Há também um princípio de coesão por trás do método de Xangai: a classe aprende como se fosse um só aluno, todos avançando no mesmo ritmo - não prosseguindo se alguém ainda estiver com dúvidas.

Os professores, por exemplo, não dividem o grupo com base na capacidade individual, nem em tarefas com dificuldade variada. Todo mundo é considerado um matemático nato e cabe aos professores tirar o melhor dos alunos.

Os estudantes com melhor desempenho são encorajados a aprofundar o conhecimento e ajudar o restante da classe, em vez de se distanciarem dos colegas menos aptos.

Enquanto essa busca pela igualdade dentro de sala é comemorada por muitos, críticos acreditam que o sistema desestimula os estudantes mais avançados, que acabariam ficando entediados.

A disposição das carteiras, porém, segue o modelo tradicional - o que, segundo críticos, não estimula a colaboração entre os pares.

"Trata-se de uma disposição rígida e pouco inspiradora", dizem.

Repetição, repetição, repetição
A repetição de conceitos também é um ingrediente fundamental da receita secreta de Xangai.

Crianças a partir de cinco anos são submetidas a testes para praticar exercícios até dominar cada conceito por meio da repetição.

Um aluno responde à pergunta de um professor e os outros repetem a resposta em uníssono. Em seguida, outra responde a uma outra pergunta e o restante repete. A sequência continua à exaustão.

Nessa rotina militar, espera-se que os estudantes aperfeiçoem o uso do vocabulário matemático - não apenas exercícios de matemática - na medida que a aula avança.

Mas as aulas são também muito interativas, destacam os especialistas.

Além disso, são curtas e harmoniosas: consistem de 35 minutos de ensino focado, seguido de 15 minutos de brincadeiras não estruturadas.

A estrela: o professor
Mas é no número de horas em sala de aula que se encontra o que é talvez o fator mais negligenciado da história de sucesso de Xangai.

Uma avaliação do modelo de ensino, publicado na semana passada pela Universidade Sheffield Hallam, mostrou que os professores só têm duas aulas diárias de 40 minutos.

O resto do dia é dedicado ao desenvolvimento profissional, incluindo feedback entre os colegas e observação das aulas.

Mas o mais importante é que um professor de matemática em Xangai passa até cinco anos na universidade estudando especificamente como ensinar matemática a alunos do ensino fundamental.

"Parte do sucesso do ensino de matemática em países como China e Cingapura vem do respeito aos professores e do tempo que eles têm para se planejar e preparar", diz o especialista em educação britânico James Bowen.

No entanto, críticos argumentam que há um descompasso entre o bem-estar dos professores e o dos estudantes.

Um estudo de 2014 sobre o bem-estar da criança, realizado pelo Instituto para o Desenvolvimento Social na NYU Xangai, revelou que enquanto a maioria das escolas está equipada com salas de aula adequadas, bibliotecas e laboratórios de informática, não têm facilidades como auditórios, ginásios ou salas de reuniões.

E cerca de 13% das crianças apresentam saúde regular ou ruim.

Mapa 3D do universo conta com mais de 1,2 milhão de galáxias

Imagem: Daniel Eisenstein e SDSS-III

Na imagem acima, cada ponto representa a posição de uma galáxia tanto quanto seis bilhões de anos no passado, dentro de apenas um vigésimo do céu que vemos acima de nós, abrangendo um segmento do universo de seis bilhões de anos-luz de largura, 4,5 bilhões de anos-luz de altura, e 500 milhões de anos-luz de espessura. O mapa contém 48.471 galáxias, o que representa cerca de 3% do que o BOSS estuda. (Há uma estimativa de que existam 100 bilhões de galáxias no universo).

A cor indica a distância relativa da Terra, na qual objetos amarelos são os mais próximos, e objetos roxos os mais distantes. As marcas cinzas são pequenas regiões sobre as quais não existem dados. As galáxias aparentam estar bastante aglomeradas, revelando superaglomerados e vazios.

Vamos colocar essa imagem em perspectiva. Vamos considerar que cada galáxia tenha uma média de 100 bilhões de estrelas. Cerca de 48.471 galáxias representam, portanto, aproximadamente 4.874.100.000.000.000 estrelas, ou um vigésimo do que foi estudado. Considerando isso, existem cerca de 100 quadrilhões de estrelas – um seguido de 18 zeros.

Imagem: Jeremy Tinker e SDSS-III

A imagem acima mostra um segmento do universo em três dimensões. O retângulo à esquerda mostra um recorde de 1.000 graus quadrados do céu contendo cerca de 120.000 galáxias, ou cerca de 10% do que foi estudado. As regiões mais claras correspondem a mais galáxias. “Vamos uma conexão dramática entre as impressões de ondas de som vistas no fundo cósmico de micro-ondas 400.000 anos após o Big Bang até o agrupamento das galáxias 7 a 12 anos bilhões de anos depois”, diz Rita Tojeiro, pesquisadora do BOSS e da Universidade de St. Andrews, em um comunicado.

Os dados do BOSS mostram que a energia escura – que dirige a expansão cosmológica – é consistente com a constante cosmológica com margem de erro de apenas 5%. Esse mapa também é totalmente consistente com o modelo cosmológico padrão (no qual o universo contém uma constante cosmológica), adicionando mais peso a essa teoria científica. Mais adiante, cosmólogos poderão usar essas informações para entender melhor as mecânicas precisas por trás da energia escura.

Contido em: http://gizmodo.uol.com.br/novo-mapa-3d-do-universo-conta-com-mais-de-12-milhao-de-galaxias/, pesquisado em 16/07/2016 as 11h00.

Os Papiros da Matemática Egípcia (Rhind e Moscou)

Papiro de Rhind (ou Ahmes)

A Matemática foi inventada e desenvolvida pelo homem em função de suas necessidades sociais. Desde a pré-história, o homem já tinha ímpetos em realizar a contagem, vivendo apenas por meio da caça e da pesca, em que eram utilizados paus, pedras e fogo. Neste período, o homem já dominava noções de mais-menos, maior-menor, algumas formas de lascamento de pedras e confecção de porretes. Com a domesticação dos animais (a velha história do pastoreiro que contava seu rebanho com pedras) surgiu a ideia de correspondência biunívoca (um a um), em que há analogia com a função bijetora.

Os grandes progressos que marcaram o fim da pré-história e que originaram a escrita verificaram-se com muita intensidade e rapidez no Egito. Por meio do grande desenvolvimento na agricultura, artesanato, comércio, entre outros até a construção das famosas pirâmides, surge a necessidade de efetuar cálculos mais rápidos e precisos, conseqüentemente, a representação através de símbolos (desenhos, escrita, números). Por volta de 2600 a.C., o Egito transformou-se no grande exportador do papiro, uma espécie de papel (este teve sua descoberta na China em 105 d.C., findando o uso do papiro), inclusive com utilidade semelhante. O encontro dos papiros proporcionou um estudo inicial da cultura egípcia.

Quase tudo o que se sabe sobre a Matemática dos antigos egípcios, se baseia em dois grandes papiros: o Papiro de Rhind e o Papiro de Moscou.

Os Papiros da Matemática Egípcia: Quase tudo o que se sabe sobre a Matemática dos antigos egípcios, se baseia em dois grandes papiros: o Papiro de Rhind e o Papiro de Moscou. Estes são compostos por exposições de problemas e suas resoluções. Foram por meio desses papiros que os cientistas compreenderam o sistema de numeração egípcia. O tal sistema baseava-se em sete números chave: 1, 10, 100, 1.000, 10.000, 100.000 e 1.000.000. Esses números eram representados pelos seguintes símbolos:  

Um traço vertical representava 1 unidade:  

Um osso de calcanhar invertido representava o número 10:  

Um laço valia 100 unidades:  

Uma flor de lótus valia 1.000:  

Um dedo dobrado valia10.000:
Com um girino os egípcios representavam 100.000 unidades:
Uma figura ajoelhada, talvez  representando um deus, valia 1.000.000:       

 Segundo o site malhatlantica: “Uma vez que estes papiros são compostos por problemas e das suas resoluções, alguns dos quais elementares, supõe-se que eles tinham intenções puramente pedagógicas e que eram basicamente destinados ao ensino dos funcionários do estado, os escribas. A partir destes temos acesso apenas a uma matemática elementar. Não se sabe se os egípcios tinham, ou não, conhecimentos matemáticos mais avançados, no entanto os monumentos por eles construídos levam a pensar que na realidade os arquitetos eram possuidores de conhecimentos não revelados nos papiros.”

O Papiro de Rhind: Em 1855, o advogado e antiquário escocês Alexander Henry Rhind aos 22 anos, viajou por razões de saúde para o Egito em busca de um clima mais ameno, e lá começou a estudar objetos da Antiguidade. Em 1858, na cidade de Luxor, comprou um grande papiro que teria sido descoberto nas ruínas de um antigo edifício de Tebas. Rhind morreu cinco anos mais tarde (1863) e o seu papiro foi adquirido pelo British Museum, Museu Britânico de Londres. Por esse motivo o papiro leva seu nome.

Também é conhecido por Papiro de Ahmes, o escriba egípcio que o copiou.

Segundo o site educ.: “O escriba diz-no que o material deriva de um original do Reino Médio, escrito entre 2.000 e 1.800 a.C. (...), e é possível que algum do conhecimento tenha vindo do famoso arquiteto e físico Imhotepy que supervisionou a construção da pirâmide do Faraó Zozer há cerca de 5.000 anos.”

Segundo Carl Boyer: “Esse papiro faltava alguns fragmentos, e o egiptólogo americano Edwin Smith comprou no Egito o que pensou que fosse um papiro médico (...). A aquisição de Smith foi doada à Sociedade Histórica de Nova York (Museu do Brooklyn) em 1932, quando os especialistas descobriram ser a parte que faltava no Papiro de Ahmes.”

O papiro, datado a cerca de 1650 a.C., escrito em hierático, da direita para a esquerda, tem aproximadamente 5,5 m de comprimento e 0,32 m de largura, contém 84 problemas e suas resoluções. 

Segundo Howard Eves:  “O Papiro Rhind é uma fonte primária rica sobre a Matemática egípcia antiga; descreve os métodos de multiplicação e divisão dos egípcios, o uso que faziam das frações unitárias, seu emprego da regra de falsa posição, sua solução para o problema da determinação da área de um círculo e muitas aplicações da matemática a problemas práticos.”

 A primeira parte do papiro parece representar um manual do cálculo matemático de regras e questões organizadas para servirem de guia aos sacerdotes egípcios, cultores da especialidade. Eis uma lista dos problemas e algumas resoluções:

1 a 6:              Divisão de 1, 2, 6, 7, 8 e 9 pães por 10 homens.

          Multiplicação de diferentes fracções por 1 + 1/2 + 1/4 ou 1 + 2/3 + 1 /3

7 a 20 21-23:  Subtrações: 1 - (2/3 + 1/15), 1 - (2/3 + 1/30) e 2/3 - (1/4 + 1/8 + 1/10 + 1/30 + 1/45).

 

         Problemas de quantidades, envolvendo equações do 1º grau com uma

24 a 29            incógnita, resolvidas pelo método da falsa posição. 

        Problemas semelhantes aos anteriores, mas mais complicados

30 a 34           (envolvendo frações) e resolvidos pelo método da divisão.

        Problemas de hekat (medida de capacidade), envolvendo equações do

35 a 38           1º. grau com uma incógnita mas ainda mais complexas que as anteriores, resolvidos  pelo método da falsa posição.

39                                     Divisão de pães.

40                                     Divisão de pães envolvendo progressões aritméticas.

41   a 43          Volumes de contentores cilíndricos de cereais.

44 a 47           Volumes de contentores paralelepipédicos de cereais. 

47                                     Tabela das frações de 1 hékat, como frações do olho de Hórus.

48  a 53           Áreas de triângulos, retângulos, trapézios e círculos.

54 e 55           Divisão relacionada com área.

56 a 60           Problemas relacionados com pirâmides (sekeds, alturas e bases) 

61 e 61B        Tabela de uma regra para encontrar 2/3 de números ímpares e frações unitárias.

62                                     Problema de proporções, sobre metais preciosos e os seu peso.

63 e 65           Divisão proporcional de pães por um número de homens.

64                                     Problema envolvendo uma progressão aritmética.

66                                    Divisão de gordura.

67                                    Proporção de gado devido a imposto.

68                                   Divisão proporcional de cereais entre grupos de homens.

69   a 78         Problemas de pesos de pão e cerveja. Proporção inversa.

79                                   Progressão geométrica de razão 7.

80   e 81         Tabelas das frações do olho de Hórus.

     Problemas (pouco claros) sobre a quantidade de comida de vários 

82 a 84        animais domésticos, como gansos e outras aves. 

Segundo Gillings: “Problemas 24 a 38":Estes problemas envolvem equações do 1º grau com uma incógnita. Os problemas 24 a 29 são resolvidos pelo método da falsa posição, que consiste em partindo de um falso valor para a incógnita chegar ao valor correto. O resultado do valor incorreto é comparado com o resultado correto e através de proporções chega-se à resposta correta.  Os problemas 30 a 34 são semelhantes aos anteriores, mas mais complicados e são resolvidos pelo método da divisão. Os problemas 35 a 38 são problemas ainda mais complicados que os anteriores, mas envolvendo medidas de capacidade (héqat), são resolvidos pelo método da falsa posição.

Problemas 24 a 30 e final dos 21 a 31

                                                Problemas 34 a 38 e final do 33 dos 21 a 31

   

Problema 24: Uma quantidade, 1/7 desta adicionada a esta, fica: 19. Solução: 16 + ½ + 1/8 

Problema 25: A quantidade e a sua ½ adicionadas dão 16. Qual é a quantidade?   Solução: 10 + 2/3 

Problema 28: A quantidade e os seus 2/3 são adicionados, e da soma um terço da soma é subtraído, e ficam 10. Qual é a quantidade?   Solução: 9

Problema 31: A quantidade, os seus 2/3, a sua ½ e o seu 1/7, adicionadas, dão 33. Qual é a quantidade?

Solução: 14 + ¼ + 1/56 + 1/97 + 1/194 + 1/388 + 1/679 + 1/776 

Problema 32: A quantidade, a sua 1/3, e a sua 1/4 adicionadas dão 2. Qual é a quantidade? Solução: 1 + 1/6 + 1/12 + 1/144 + 1/228 

Problema 33: A quantidade, os seus 2/3, a sua  ½, e a sua 1/7 adicionadas dão 37. Qual é a quantidade? 

Solução: 16 + 1/56 + 1/679 + 1/776 

Problemas 40, 64 e 79: O problema 40 é sobre a divisão de pães e o problema 64 sobre a divisão de cevada, ambos envolvem progressões aritméticas. As tabelas apresentadas em 79 envolvem a progressão geométrica de razão 7.

Problemas 39 e 40 e final dos 34, 36, 37 e 38

Problema 40: 100 pães para 5 homens. 1/7 dos 3 homens acima, para os 2 homens abaixo. Qual é a diferença das porções recebidas?

Problema 64: Exemplo de distribuições diferentes. Se te digo, divide 10 héqats de cevada por 10 homens, de tal maneira que a diferença entre cada homem e o seu vizinho seja em héqats de cereal, 1/8, qual é a parte que cabe a cada homem?  

Problema 79: Inventário de uma casa 

                                               Coluna 1                                           Coluna 2  

1		2801	Casas	7
2		5602	Gatos	49
3		11204	Ratos	343
Total		19607	Trigo	2301
			Héqat	16807

                                                                                  Total                                 19607

Problema 48: Compara a área do círculo e do quadrado circunscrito. 

Solução: O círculo de diâmetro 9: 64 setat, o quadrado de lado 9: 81 setat

Problemas 69 a 78: Estes problemas dizem, todos, respeito a questões sobre o peso. O peso é a razão entre o número de pães confeccionados ou o número de jarros de cerveja produzidos e o número de héqats de cereal utilizado na sua produção. Os egípcios ao produzirem cerveja utilizavam mais cereal do que ao produzirem pão, assim a mesma quantidade de cereja produzia mais pães do que jarros de cerveja. Os valores de peso de cerveja variavam entre 1 e 4 (de acordo com os problemas constantes dos papiros de Rhind e de Moscou) enquanto que os do pão variavam entre 5 e 45.    

Problemas 71 a 79 e final dos 65 e 67 a70

Problema 69: 3 ½ héqats de farinha são transformados em 80 pães. Descubra a quantidade de farinha em cada pão e o peso. 

Solução: 14 ro em cada pão e o peso é 22 + 2/3 + 1/7 + 1/21

Nota: Há 320 ro em cada héqat. 

Problema 71: De uma jarra de cerveja se tira ¼ do conteúdo e se troca por água. 

Determinar o novo peso da cerveja, supondo que a cerveja inicial era o produto de meio héqat de cereal. 

Solução: 2 + 2/3 

Problema 72

100 pães de peso 10 devem ser trocados por pães de peso 45. Quantos pães deste tipo haverá?  Solução: 450.

Problema 73: 100 pães de peso 10 devem ser trocados por pães de peso 15. Quantos pães destes tipo é que haverá?  Solução: 150.

Problema 74: 1000 pães de peso 5 devem ser trocados por um número de pães de peso 20 e pelo mesmo número de pães de peso 30.  pães de peso 15. Quantos pães de cada tipo é que haverá?  Solução: 1200.

Problema 75: 155 pães de peso 20 devem ser trocados por um número de pães de peso 30. Quantos pães deste tipo é que haverá?  Solução: 232 + ½” 

Papiro de Moscou

Após falarmos um pouco sobre o Papiro de Rhind ou Ahmes, agora vamos a outro papiro egípcio que também foi muito importante para o estudo sobre a História da Matemática: O Papiro de Moscou. 

O Papiro de Moscou, também chamado de Papiro de Golenischev em homenagem ao egiptólogo e colecionador russo Abraão V.S. Golenischev, que o comprou no Egito em 1893. Foi comprado em 1917 pelo Museu de Belas Artes de Moscou, aí passou a ser conhecido como Papiro de Moscou. O papiro foi escrito por um escriba desconhecido, tem cerca de 5 m de comprimento e 0,08 m de largura e contém 25 problemas, mas devido ao seu estado de degradação é impossível interpretar muito deles. Neste papiro é apresentada uma forma de cálculo do volume do tronco de pirâmide de base quadrada. Eis uma lista dos problemas e algumas resoluções:

1 a 2                       Ilegíveis.

3                                             Altura de um poste de madeira (pouco claro)

4                                            Área de um triângulo

5, 8,  9, 13 e 22    Pesos de pães e cerveja

6                                           Área de um retângulo.

7 e 17                   Área de um triângulo

10                                       Área de uma superfície curva 

11                                       Pães e cestos (pouco claro)

12                                       Pesos de cerveja (pouco claro)                                              

14                        Volume de uma pirâmide truncada

15 e 16                Pesos de cerveja.

18                        Medidas de panos em palmos e cúbitos(pouco claro) 

19                        Equação linear.

20                                       Pesos de 1000 pães e frações de Hórus. 

21                                       Mistura de pão para sacrifício

23                                      Cálculo do trabalho de um sapateiro (pouco claro)

24                                      Intercâmbios de pães e cerveja

25                                      Problema que dá origem à equação 2x + x = 9

             Segundo Gillins: “Problemas 4, 6, 10 e 14". Estes problemas envolvem áreas e volumes. Os problemas 4 e 6 são sobre a área de um triângulo e de um retângulo, respectivamente. O problema 10 envolve a área de superfície do que parece ser um cesto de diâmetro 4,5. No problema 14 pede-se para calcular a área de uma figura. A figura parece ser um trapézio isósceles, no entanto é na realidade um tronco de pirâmide quadrangular. 

      Problema 4: Descobre a área de um triângulo de altura 10 e base 4.

Problema 6 : Método do cálculo do retângulo. Se é dito, um retângulo de área 12, largura ½ + ¼ do comprimento.

Resolução: 

Calcula ½ + ¼ até obter 1. Resultado 1 + 1/3.

Calcula 1 + 1/3 de 12. Resultado 16. 

Calcula então o seu ângulo [raiz quadrada]. Resultado 4 para o comprimento e 3 para a largura. 

Problema 10: Exemplo do cálculo de um cesto. É dito que um cesto com uma abertura de 4 + ½ [de diâmetro. Qual a sua superfície? 

Resolução: 

Calcula 1/9 de 9, porque o cesto é metade de um ovo. Resultado 1.

Toma o que sobra que é 8. Calcula 1/9 de 8. Resultado 2/3 + 1/6 + 1/18. Calcula o que resta destes 8 depois de tirares 2/3 + 1/6 + 1/8: Resultado 7 + 1/9.

Multiplica 7 + 1/9 por 4 + 1/2: Resultado 32.

     Problema 14 : Método de calcular um tronco de pirâmide. Se é dito, um tronco de pirâmide tem 6 cúbitos de altura, 4 cúbitos de base, por 2 cúbitos no topo.

Resolução: 

Calcula com este 4, quadrando. Resultado 16.

Dobra este 4. Resultado 8.

Calcula com o este  2, quadrando. Resultado 4.

Adiciona este 16 com este 8 e com este 4. Resultado 28.

Calcula 1/3 de 6. Resultado 2.

Calcula o dobro de 28. Resultado 56.
É 56. Encontraste o resultado certo.

         Problema 19 e 21: O problema 19 envolve a seguinte equação do 1º grau, escrita na notação atual, 1½ x + 4 = 10. O problema 21 é sobre uma mistura de pão para sacrifício.

     Problema 19: Método de calcular uma pilha. 1 + 1/2 vezes junto com 4, deu 10.

Qual é esta pilha? 

Resolução: 

Calcula o excesso destes 10 sobre estes 4, é 6.

Calcula com 1+ ½ até obteres 1.

Resultado 2/3.

Calcula 2/3 destes 6.

Resultado 4.

          Problema 21: Método de calcular a mistura dos pães para sacrifícios.

Se te dizem 20 medidas como 1/8 de um heqát e 40 medidas como 16 heqát.

Resolução: 

Calcula 1/8 de 20. Resultado 2 + ½.

Calcula 1/16 de 40. Resultado 2 + ½.

O total de estas duas metades é 5.

Calcula a soma das outras duas metades. Resultado 60.

Divide 5 por 60. 

Resultado 1/12.  

A mistura é 1/12.