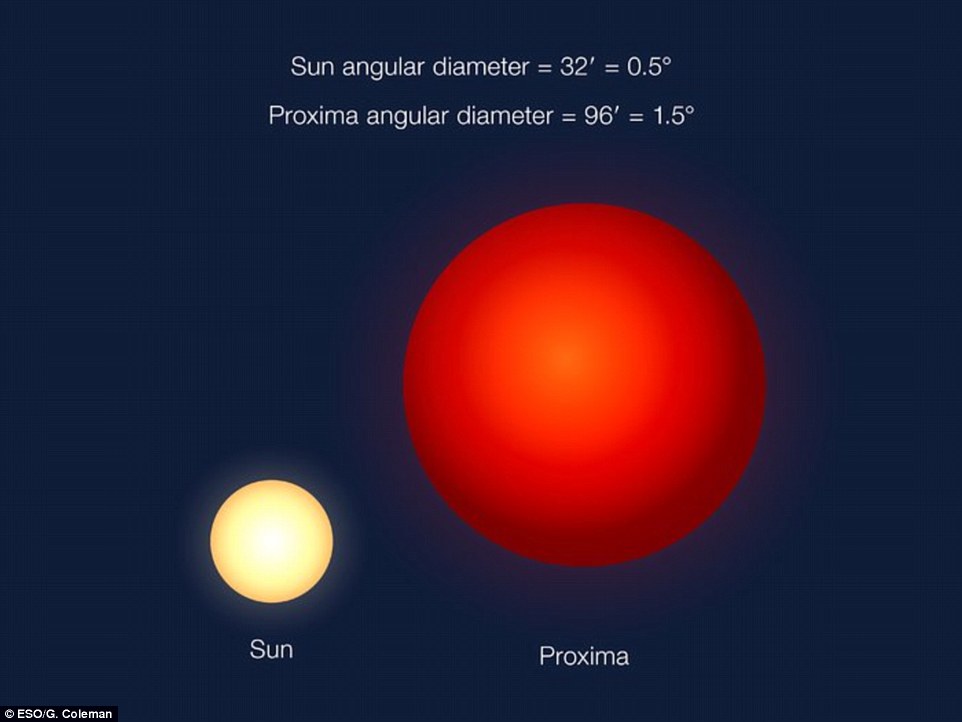
Um osso de calcanhar invertido representava o número 10:
Um laço
valia 100 unidades:
Uma flor de
lótus valia 1.000:
Um dedo dobrado valia10.000:
Com um girino os egípcios representavam 100.000 unidades:
Uma figura ajoelhada, talvez representando um deus, valia 1.000.000:
Segundo o site malhatlantica: “Uma vez que estes papiros são
compostos por problemas e das suas resoluções, alguns dos quais elementares,
supõe-se que eles tinham intenções puramente pedagógicas e que eram basicamente
destinados ao ensino dos funcionários do estado, os escribas. A partir destes
temos acesso apenas a uma matemática elementar. Não se sabe se os egípcios
tinham, ou não, conhecimentos matemáticos mais avançados, no entanto os
monumentos por eles construídos levam a pensar que na realidade os arquitetos
eram possuidores de conhecimentos não revelados nos papiros.”
O Papiro de Rhind: Em 1855, o advogado e antiquário escocês
Alexander Henry Rhind aos 22 anos, viajou por razões de saúde para o Egito em
busca de um clima mais ameno, e lá começou a estudar objetos da Antiguidade. Em
1858, na cidade de Luxor, comprou um grande papiro que teria sido descoberto
nas ruínas de um antigo edifício de Tebas. Rhind morreu cinco anos mais tarde
(1863) e o seu papiro foi adquirido pelo British Museum, Museu Britânico de
Londres. Por esse motivo o papiro leva seu nome.
Também é conhecido por Papiro de Ahmes,
o escriba egípcio que o copiou.
Segundo o site educ.: “O escriba diz-no que o material deriva de um original do
Reino Médio, escrito entre 2.000 e 1.800 a.C. (...), e é possível que algum do
conhecimento tenha vindo do famoso arquiteto e físico Imhotepy que
supervisionou a construção da pirâmide do Faraó Zozer há cerca de 5.000 anos.”
Segundo Carl Boyer: “Esse papiro faltava alguns fragmentos, e o egiptólogo
americano Edwin Smith comprou no Egito o que pensou que fosse um papiro médico
(...). A aquisição de Smith foi doada à Sociedade Histórica de Nova York (Museu
do Brooklyn) em 1932, quando os especialistas descobriram ser a parte que
faltava no Papiro de Ahmes.”
O papiro, datado a cerca de 1650 a.C., escrito
em hierático, da direita para a esquerda, tem aproximadamente 5,5 m de
comprimento e 0,32 m de largura, contém 84 problemas e suas resoluções.
Segundo Howard Eves: “O Papiro Rhind é uma fonte primária rica
sobre a Matemática egípcia antiga; descreve os métodos de multiplicação e
divisão dos egípcios, o uso que faziam das frações unitárias, seu emprego da
regra de falsa posição, sua solução para o problema da determinação da área de
um círculo e muitas aplicações da matemática a problemas práticos.”
A primeira parte do papiro parece representar
um manual do cálculo matemático de regras e questões organizadas para servirem
de guia aos sacerdotes egípcios, cultores da especialidade. Eis uma lista dos
problemas e algumas resoluções:
1 a 6: Divisão
de 1, 2, 6, 7, 8 e 9 pães por 10 homens.
Multiplicação de diferentes fracções por 1 + 1/2 + 1/4 ou
1 + 2/3 + 1 /3
7 a 20 21-23: Subtrações: 1 - (2/3 +
1/15), 1 - (2/3 + 1/30) e 2/3 - (1/4 + 1/8 + 1/10 + 1/30 + 1/45).
Problemas de quantidades, envolvendo equações do 1º grau
com uma
24 a 29 incógnita, resolvidas
pelo método da falsa posição.
Problemas semelhantes aos anteriores, mas mais complicados
30 a 34 (envolvendo frações) e resolvidos pelo método da divisão.
Problemas de hekat
(medida de capacidade), envolvendo equações do
35 a 38 1º. grau com uma incógnita mas
ainda mais complexas que as anteriores, resolvidos pelo método da falsa
posição.
39 Divisão de pães.
40 Divisão de pães envolvendo progressões
aritméticas.
41 a 43 Volumes de contentores cilíndricos de
cereais.
44 a 47 Volumes de contentores paralelepipédicos de
cereais.
47 Tabela das frações de 1 hékat, como frações do
olho de Hórus.
48 a 53 Áreas de triângulos, retângulos, trapézios
e círculos.
54 e 55 Divisão relacionada com área.
56 a 60 Problemas relacionados com pirâmides (sekeds,
alturas e bases)
61 e 61B Tabela de uma regra
para encontrar 2/3 de números ímpares e frações unitárias.
62 Problema de proporções, sobre metais preciosos e
os seu peso.
63 e 65 Divisão proporcional de pães por um número
de homens.
64 Problema envolvendo uma progressão aritmética.
66 Divisão de gordura.
67 Proporção de gado devido a imposto.
68 Divisão proporcional de cereais entre grupos de
homens.
69 a 78 Problemas de pesos de pão e cerveja. Proporção inversa.
79 Progressão geométrica de razão 7.
80 e 81 Tabelas das frações do olho de Hórus.
Problemas (pouco claros) sobre a quantidade de comida de
vários
82 a 84 animais domésticos,
como gansos e outras aves.
Segundo Gillings: “Problemas 24 a 38":Estes problemas envolvem equações do 1º
grau com uma incógnita. Os problemas 24 a 29 são resolvidos pelo método da
falsa posição, que consiste em partindo de um falso valor para a incógnita
chegar ao valor correto. O resultado do valor incorreto é comparado com o
resultado correto e através de proporções chega-se à resposta correta. Os problemas 30 a 34 são semelhantes aos
anteriores, mas mais complicados e são resolvidos pelo método da divisão. Os
problemas 35 a 38 são problemas ainda mais complicados que os anteriores, mas
envolvendo medidas de capacidade (héqat),
são resolvidos pelo método da falsa posição.
Problemas 24 a 30 e final dos 21 a 31
Problemas 34 a 38 e final do
33 dos 21 a 31
Problema 24: Uma quantidade, 1/7 desta adicionada a esta, fica:
19. Solução: 16 + ½ + 1/8
Problema 25: A quantidade e a sua ½ adicionadas dão 16. Qual é a
quantidade? Solução: 10 + 2/3
Problema 28: A quantidade e os seus 2/3 são adicionados, e da
soma um terço da soma é subtraído, e ficam 10. Qual é a quantidade? Solução:
9
Problema 31: A quantidade, os seus 2/3, a sua ½ e
o seu 1/7, adicionadas, dão 33. Qual é a quantidade?
Solução: 14 + ¼
+ 1/56 + 1/97 + 1/194 + 1/388 + 1/679 + 1/776
Problema 32: A quantidade, a sua 1/3, e a sua 1/4 adicionadas dão 2.
Qual é a quantidade? Solução: 1 +
1/6 + 1/12 + 1/144 + 1/228
Problema 33: A quantidade, os seus 2/3, a sua ½, e a sua 1/7 adicionadas dão 37. Qual é a
quantidade?
Solução: 16 +
1/56 + 1/679 + 1/776
Problemas 40, 64 e 79: O problema 40 é sobre a divisão de pães
e o problema 64 sobre a divisão de cevada, ambos envolvem progressões
aritméticas. As tabelas apresentadas em 79 envolvem a progressão geométrica de
razão 7.
Problemas
39 e 40 e final dos 34, 36, 37 e 38
Problema 40: 100 pães para 5 homens. 1/7 dos 3 homens acima, para os 2
homens abaixo. Qual é a diferença das porções recebidas?
Problema 64: Exemplo
de distribuições diferentes. Se te digo, divide 10 héqats de cevada por 10 homens, de tal maneira que a diferença
entre cada homem e o seu vizinho seja em héqats
de cereal, 1/8, qual é a parte que cabe a cada homem?
Problema 79: Inventário de uma casa
Coluna
1 Coluna
2
1
|
|
2801
|
Casas
|
7
|
2
|
|
5602
|
Gatos
|
49
|
3
|
|
11204
|
Ratos
|
343
|
Total
|
|
19607
|
Trigo
|
2301
|
|
|
|
Héqat
|
16807
|
Total 19607
Problema 48: Compara a área do círculo e do quadrado circunscrito.
Solução: O
círculo de diâmetro 9: 64 setat, o
quadrado de lado 9: 81 setat
Problemas 69 a 78: Estes problemas dizem, todos, respeito a
questões sobre o peso. O peso é a razão entre o número de pães
confeccionados ou o número de jarros de cerveja produzidos e o número de héqats de cereal utilizado na sua
produção. Os egípcios ao produzirem cerveja utilizavam mais cereal do que ao
produzirem pão, assim a mesma quantidade de cereja produzia mais pães do que
jarros de cerveja. Os valores de peso
de cerveja variavam entre 1 e 4 (de acordo com os problemas constantes dos
papiros de Rhind e de Moscou) enquanto que os do pão variavam entre 5 e
45.
Problemas
71 a 79 e final dos 65 e 67 a70
Problema 69: 3 ½ héqats de farinha são transformados em 80 pães. Descubra a
quantidade de farinha em cada pão e o peso.
Solução: 14 ro em cada pão e o peso é 22 + 2/3 + 1/7 + 1/21
Nota: Há 320 ro em cada héqat.
Problema 71: De uma jarra de cerveja se tira ¼ do conteúdo e se troca
por água.
Determinar o novo peso da cerveja, supondo que a cerveja
inicial era o produto de meio héqat
de cereal.
Solução: 2 + 2/3
Problema 72
100
pães de peso 10 devem ser trocados
por pães de peso 45. Quantos pães
deste tipo haverá? Solução: 450.
Problema 73: 100
pães de peso 10 devem ser trocados
por pães de peso 15. Quantos pães destes tipo é que
haverá? Solução: 150.
Problema 74: 1000
pães de peso 5 devem ser trocados por
um número de pães de peso 20 e pelo mesmo número de pães de peso 30. pães de peso
15. Quantos pães de cada tipo é que
haverá? Solução: 1200.
Problema 75: 155
pães de peso 20 devem ser trocados por
um número de pães de peso 30. Quantos
pães deste tipo é que haverá? Solução: 232 + ½”


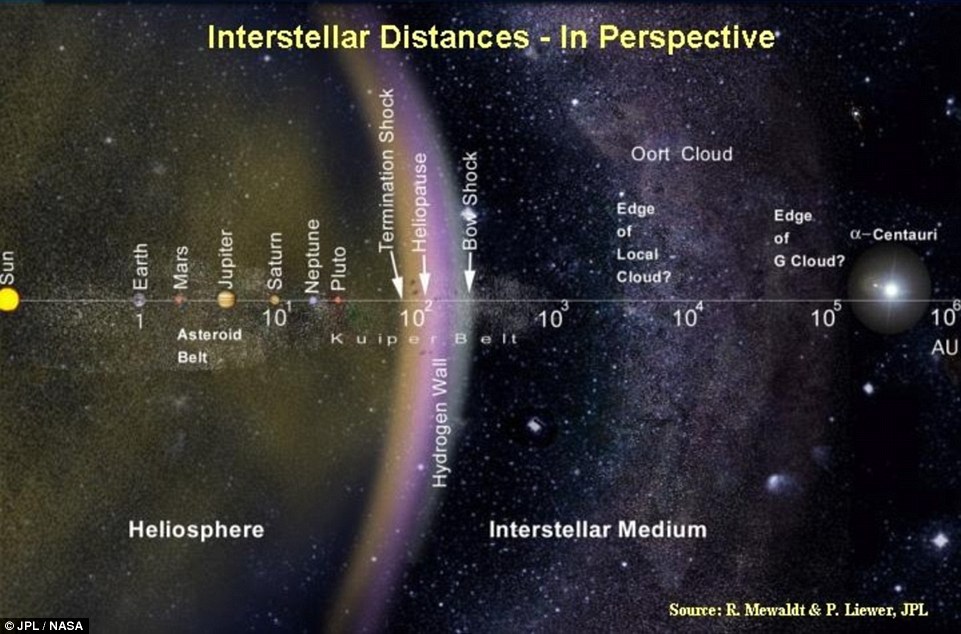
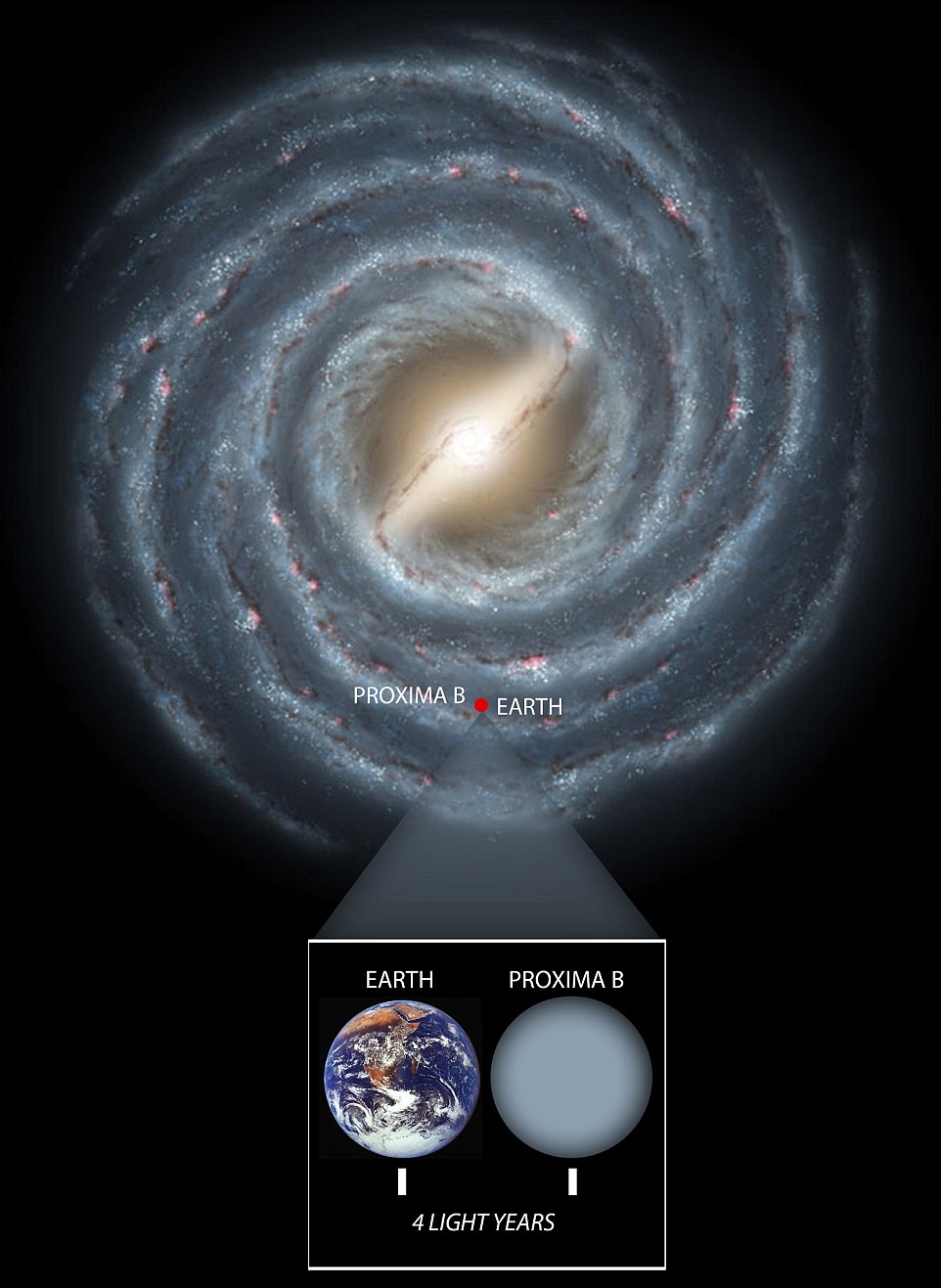
 Acredita-se que a
temperatura da superfície de Proxima b poderia estar entre -90 graus Celsius e
30°C. Porque recebe potentes raios ultravioletas da estrela, qualquer vida que
tenha surgido ali teria de ser evoluída o suficiente para suportar a radiação.
Além disso, uma atmosfera potencialmente composta por elementos simples, como a
água e dióxido de carbono – que são necessários para a formação de ciclos
bioquímicos (ou vida) – poderiam estar presentes e interagindo entre si na
superfície do planeta.
Acredita-se que a
temperatura da superfície de Proxima b poderia estar entre -90 graus Celsius e
30°C. Porque recebe potentes raios ultravioletas da estrela, qualquer vida que
tenha surgido ali teria de ser evoluída o suficiente para suportar a radiação.
Além disso, uma atmosfera potencialmente composta por elementos simples, como a
água e dióxido de carbono – que são necessários para a formação de ciclos
bioquímicos (ou vida) – poderiam estar presentes e interagindo entre si na
superfície do planeta.