A medida de um ângulo é dada em graus e representada por um número seguido do símbolo “°”. Ela também pode ser relacionada a outros tipos de medidas, por exemplo a números reais e a radianos. Um ângulo é relacionado a um número real por meio das razões trigonométricas seno, cosseno e tangente no ciclo trigonométrico.
Um ângulo é relacionado a radianos por meio do comprimento de arcos de circunferências. Por isso essa relação também pode ser feita no ciclo trigonométrico.
Definição de radiano
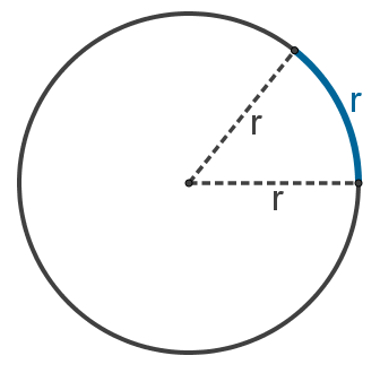
Dada uma circunferência de raio r e considerando um de seus arcos, cujo comprimento também é igual a r, dizemos que esse arco tem o comprimento igual a 1 rad (radiano).
Em outras palavras, 1 radiano é igual a um arco de medida r de uma circunferência cujo raio mede r. Sabendo que todo arco está relacionado a um ângulo central, as medidas em radianos também estarão.
A imagem a seguir mostra um círculo e o arco que possui medida igual a 1 rad.
Exemplo: Um círculo possui raio igual a 10 centímetros. Qual a medida, em radianos, do arco cujo comprimento é igual a 15 centímetros?
Para resolver esse problema, basta lembrar que 1 radiano é igual ao raio da circunferência. Nesse caso, o arco que possui 10 centímetros mede 1 radiano. Quanto medirá, nesse mesmo círculo, um raio que possui 15 centímetros? Para resolver esse problema, utilize regra de três:
1 = 10
x 15
x 15
10x = 15
x = 15
10
10
x = 1,5 rad
Radianos em função de pi
É sempre possível relacionar um ângulo central a uma medida de um arco. Assim, sempre dá para associar um ângulo central a uma medida em radianos. Com o objetivo de relacionar o ângulo de 180°, por exemplo, a uma medida em radianos, usamos regra de três. Para tanto, lembre-se de que 180° é igual à meia circunferência, por isso seu comprimento é πr.
1 = r
x πr
x πr
xr = πr
x = π
Ou seja: 180° = π rad.
As medidas dos outros ângulos, dadas em radianos, podem ser todas obtidas a partir dessa relação, usando regra de três.
Com base nesse conhecimento, podemos concluir que existem π radianos em um semicírculo de 180°. Portanto, a medida do ângulo central relativo a 1 radiano é, para todo círculo ou circunferência, aproximadamente:
1 rad = 180° = 57,2958
π
π