O fascínio pelo número de ouro, data de há mais de 2 000 anos. Os "antigos" aperceberam-se que a arte e a arquitetura baseadas na razão de ouro, eram invulgarmente agradáveis à vista. A razão de ouro começou por ser definida em termos geométricos.
O número de ouro pode ser encontrado através da razão da largura e do comprimento de um retângulo de ouro.
Mas antes de prosseguirmos, iremos explicar o que se entende por retângulo de ouro.
Veja um vídeo abaixo: (Parte do filme Donald no pais da matemágica)
Veja um vídeo abaixo: (Parte do filme Donald no pais da matemágica)
Denomina-se retângulo de ouro, um retângulo que, quando é dividido em duas partes e em que uma dessas partes seja um quadrado, então o que resta terá que ser um retângulo com as mesmas proporções do retângulo inicial.
Consideremos então o seguinte retângulo de ouro:
Se retirarmos a este retângulo o quadrado de lado x ( o quadrado a ), obtém-se o novo retângulo de ouro (o retângulo b) de dimensões x e y – x. Repetindo a operação, obtém-se a seguinte sequência de retângulos de ouro (retângulo de cor amarela):

O processo anterior pode-se realizar de forma inversa. Em vez de se ir dividindo o retângulo inicial num retângulo de ouro e num quadrado, partir-se-á de um quadrado de forma a obter sucessivos retângulos de ouro:
Esta figura mostra, como se pode desenhar uma espiral, unindo quartos de círculos em cada novo quadrado (inscrito no retângulo de ouro). A espiral obtida é conhecida como a espiral de Fibonacci.
|
O número de ouro tem o valor:
 Como se lembram da secção da Sucessão de Fibonacci, temos a seguinte sequência de números 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233....
Como se lembram da secção da Sucessão de Fibonacci, temos a seguinte sequência de números 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233....Se dividirmos cada um destes números pelo seu antecedente, reparamos que essa razão vai tender para um certo valor.
Isto é, se fizermos F2/F1=1; F3/F2=2; F4/F3=1,5; F5/F4=1,6(6); F6/F5=1,6 e se continuarmos assim sucessivamente, obtemos a seguinte sequência de números:
1,000 000; 2,000 000; 1,500 000; 1,666 666; 1,600 000; 1.625 000; 1,615 385; 1,619 048; 1,617 647; 1,618 182; 1,617 978; 1,618 056; 1,618 026; 1,618 037; 1,618 033; ...
Graficamente podemos ver:
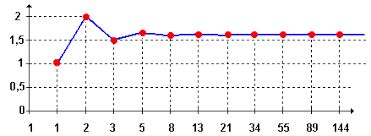
Então Fn+1/Fn aproxima-se cada vez mais de j(Phi).
Graficamente podemos ver:
Então Fn+1/Fn aproxima-se cada vez mais de j(Phi).
Esta expansão decimal prolongar-se-á sem nunca se repetir (logo é um número irracional).
De fato, quando se prolongam estas "razões de Fibonacci" indefinidamente, o valor gerado aproxima-se cada vez mais do número de ouro.
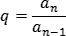
Agora vamos a definição de uma PG: Progressão geométrica é caracterizada por ter seus termos, a partir do segundo, obtidos pelo produto de q (razão da PG) com o termo anterior.
Fórmula da Razão da PG
A chamada razão da PG é uma constante representada geralmente pela letra ‘q’. É a partir da razão da PG que será determinado todos os termos, portanto ela é parte fundamental da PG.
A razão da pg (q), também conhecida como razão geométrica, é calculada fazendo a divisão de qualquer termo, exceto o 1º termo, pelo termo anterior. A fórmula da razão da PG é:
A razão da pg (q), também conhecida como razão geométrica, é calculada fazendo a divisão de qualquer termo, exceto o 1º termo, pelo termo anterior. A fórmula da razão da PG é:
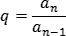
Logo o número de ouro é uma razão de uma PG ?
Contido em: http://fibonaccipaepg.blogspot.com.br/2011/06/o-numero-de-ouro-e-fibonacci_28.html, pesquisado em 16/02/2014 as 14h00.



.jpg)
.jpg)
.jpg)
.jpg)